Book Reading: Any Classical Mechanics Book

4 Oct 22 - Notes: Lagrangian Dynamics#

Newtonian Mechanics is an incredibly useful model of the natural world. In fact, it wasn’t until the mid 1970s that we were able to truly test Einstein’s gravity as a true replacement for Newton. That being said, for most terrestrial situations (macroscopic objects moving at low speeds), Newton’s mechanics is very good. However, the problem with Newton is that it requires a few things:

  1. We must be able identify each interaction on the object or model an average behavior from many littler interactions (e.g., models of friction vs. detailed E&M forces)

  2. We must be able to mathematically describe the size and direction of the interaction at all times we want to model

  3. We must be able to vectorially add the interactions to produce the net force \(\sum_i \vec{F}_i = \vec{F}_{net}\).

In many cases, we can do this. But consider the picture below of a bead sliding inside a cone. How would you write down the contact force between the cone and the bead for all space and time?

Cone

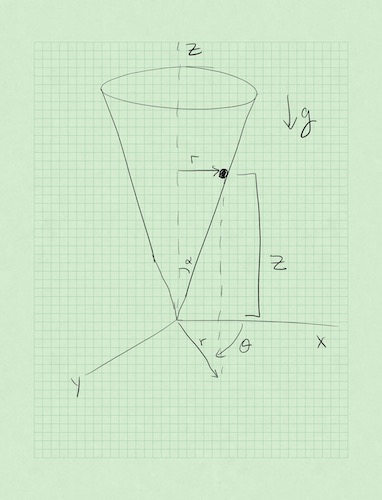
Enter the Lagrangian Mechanics, an equivalent descirption of Newton’s mechanics developed through several adbances in physics and mathematics in the 17th and 18th centuries. Some of the major contributors included Newton, Gottfried Wilhelm Leibniz, Pierre Louis Moreau de Maupertuis, Guillaume de l’Hôpital, Jacques Bernoulli, Jean Bernoulli, and Jean D’Alembert. This period of the development of mechanics was foundational to the development of concepts like the action and phase space as well as approaches like variational analysis, which formed the basis for dynamical systems (phase space describes real motion), quantum mechanics (quantize the action), and perturbation theory (approximate answers can be iteratively sought).

This analysis is grounded in optimization or rather extremization. The idea is as follows:

  1. Consider all potential paths a system can take through phase space

  2. Time each of them between the same two points in phase space

  3. The one that minimizes the action integral over that time/space is the one the system takes

This might seem magical! But it’s truly a deep connection to the energetics of the system, which limit the the relevant equations of motion by both the number of degrees of freedom (ways the system can move) and the constraints equation (things that influence the motion).

Parth G. has a lovely video below in his dulcet tone about the basics of this as we talked in class.

from IPython.display import YouTubeVideo
YouTubeVideo("KpLno70oYHE", 800, 600)

My notes go into detail on the development of the Lagrangian problem. But practice is the best approach.

Book Readings#

This reading is useful preparation for reminding yourself of Lagrangian Dynamics.

Handwritten Notes#

Here are my handwritten notes on coupled oscillations and normal modes.

Video Resources#

If you are a feeling that you would like a little direct instruction on this, this lecture is great. Lots of examples!

from IPython.display import YouTubeVideo
YouTubeVideo("zhk9xLjrmi4", 800, 600)