Project 3
Contents
Project 3#
Project 3 will expand upon our work in normal mode analysis. You need to pick an oscillation problem with linear restoring for 3 or more objects (e.g., longitudinal oscillations of 3 or more SHOs) and perform an analysis using normal modes to investigate the dynamics of those oscillators. You can reproduce the work we’ve done in class and extend it. But you can also consider other oscillators or oscillations (e.g., transverse oscillations or a small lattice). I will post resources for that below.
What do you need to do?#
Develop a computational essay that investigates the physics of your system of interest. You should be able t:
Set it up using a Lagrangian
Produce a matrix that describes the system, and
Extract the normal mode frequencies and amplitudes.
We have illustrated all of that work in class. So how do we go further? We have not done these but they exploit the linearity of the model.
You can then need to model the dynamics of the system (that is, provide it with initial conditions and let it move).
Finally, show that by using the normal modes show that you can reproduce the same motion by adding/subtracting contributions of the normal modes.
Resources#
Potential Projects Ideas#
Coupled linear simple harmonic oscillators moving in the transverse (perpendicular to springs) way (focus on linear restoring)
Coupled pendulums in a linear regime (coupled triple oscillator; or coupled horizontally with springs)
Coupled LC circuits
Models of plasmas oscillations in ionosphere
Molecular vibrations (e.g., tri-atomic molecules)
Tough and group worthy - The Loaded String (A beaded string with a finite number of beads), Piano/guitar harmonics and chords
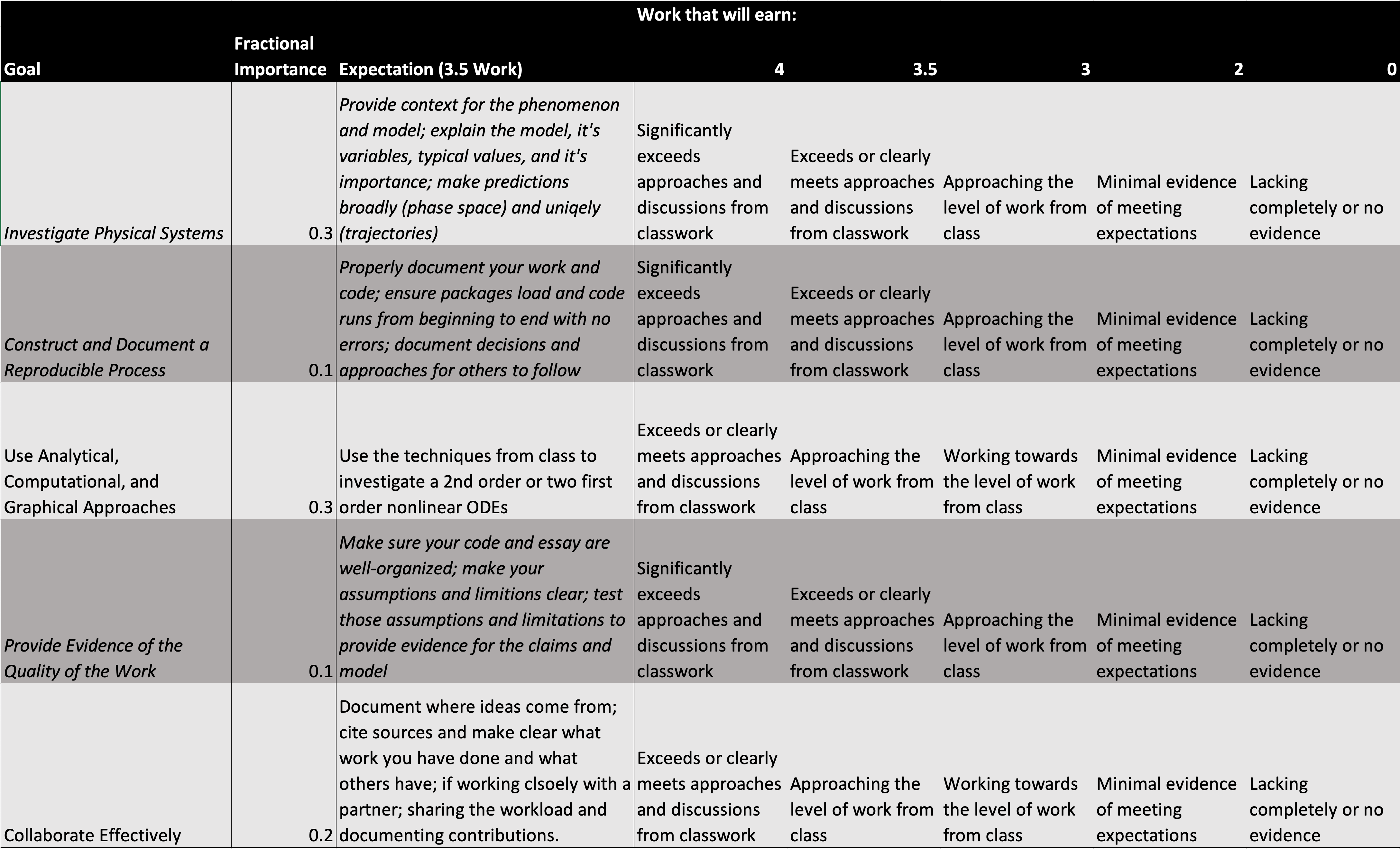
Rubric#
Our rubric will be the same as project 1 and 2.
Right click and open in new tab for large version