Project 1
Contents
Project 1#
Project 1 will focus on the the topic of ordinary differential equations in physics. Differential equations are often how we describe nature because nature often changes continuously (quantum mechanics notwithstanding). We focused in class on the harmonic oscillator and its variants. Your job is to develop a project that investigates some nonlinear differential equation of your choosing. My expectation is that this ODE is nonlinear, at least 2nd order or two coupled 1st order equations, and that is of interest to you personally or professionally. I will provide a list of potential candidates.
What do you need to do?#
Think about the ways we have explored things in class. This is meant to be an introduction to making a project, so my expectation is that the projects will get more involved and interesting over time. That is, as you learn how to do things, you will apply new ideas and do more exploration on your own. We will also reflect on our project rubric and make changes to it as you get more experience and can do more cool things.
But for this first project, I have a list of tasks that you have experienced in class:
Describe the differential equation.
what is it
what does it model
what assumptions and limitations are baked into it
Investigate it analytically as best you can
Take limits on the nonlinear aspects
Investigate approximate behaviors
Make claims about what should happen in different regimes (based on limits)
Develop a computational investigation to compliment the analytics
Create a phase space diagram
Describe qualitatively important behaviors and regimes in which they occur
Compare to your analytical work
Compute trajectories in the space and describe the evolution
Produce visualizations of you work
Make graphs that are labeled and titled appropriately for your claims
Add mathematics to the notebook is you see fit (\(LaTeX\), handwritten, typed are all ok)
Document your work
We should be able to run your notebooks and get exactly what you want us to
Comment everything
Candidate ODEs#
Wikipedia’s list of famous equations https://en.wikipedia.org/wiki/List_of_nonlinear_ordinary_differential_equations
Consider: the Chandrasekhar equation, the Duffing model, the Langmuir equation, the Rayleigh equation, the Van Der Pol oscillator
Strogatz’s Nonlinear Dynamics and Chaos
Check out Chapters 4-5 (SCAN COMING). There are many interesting examples and problem setups you could use.
Think about other systems that are described mathematically as an ODE
Predator-prey models, Pursuit models, Fireflies, etc.
Rubric#
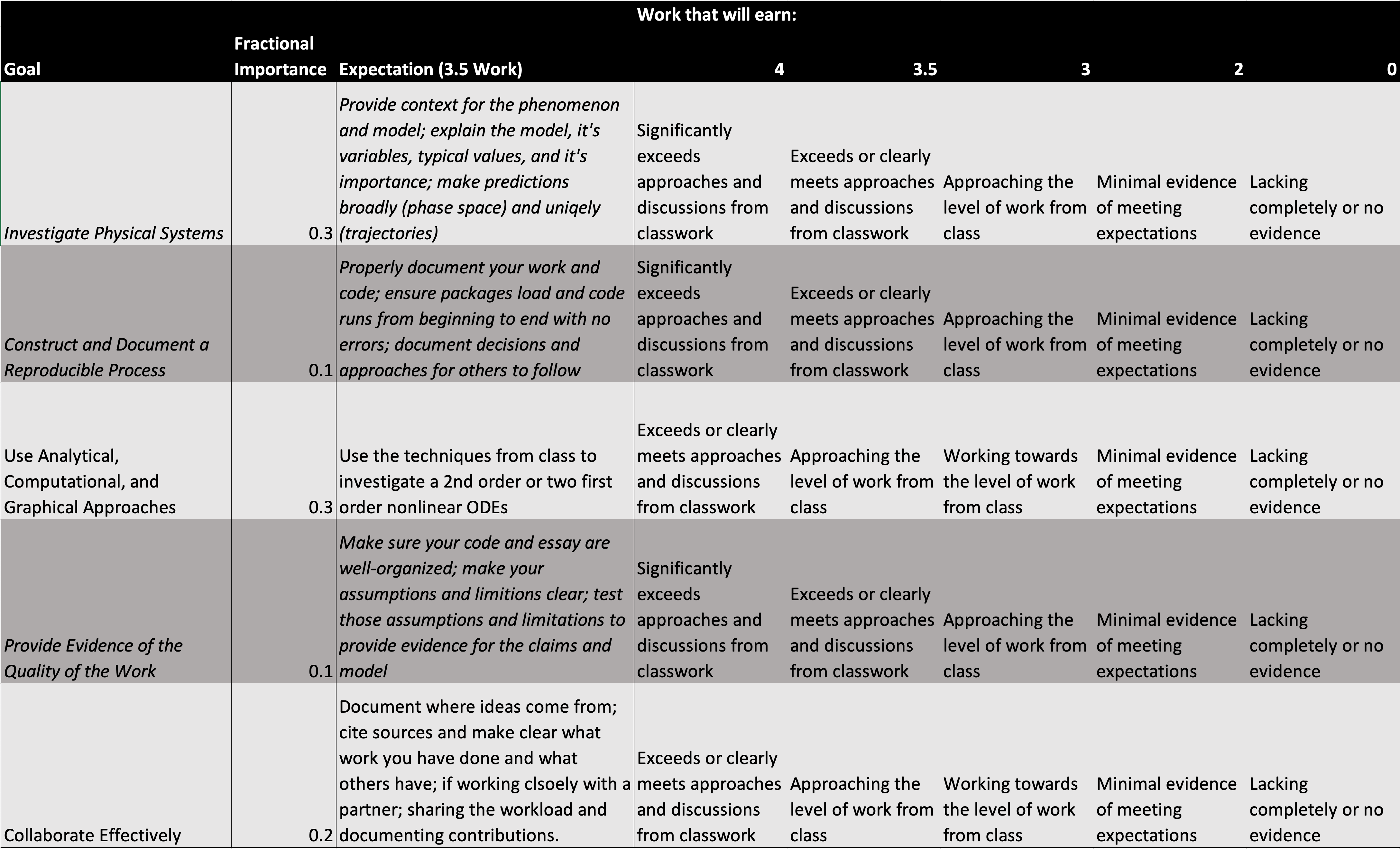
Based on our discussion in class, we will emphasize Prediction and Explanation, Reproducibility and Documentation, and Presentations and Validation for this project. It appears we had lots of ideas for what good work in those areas might look like. This means we will have slightly more rigorous expectations on those pieces. Below is the rubric we will use. I have marked the elements that we will scrutinize more closely with italics.
Right click and open in new tab for large version