29 Sept 22 - Activity: Lagrangian Dynamics#

Motivation to be completed later…

Here you will practice using the Lagrangian for increasingly complex systems. We start with the SHO and move forward from there.

Using Lagrangian dnymaics can feel like magic. In fact, this is video of me from 2002 when I learned to use this approach:

mind blown cat gif

But we will step through the levels of complexity with these examples to make sure we all understand how to make use of them.

Lagrange meme

Getting Started#

Simple Harmonic Oscillator#

✅ Do this

  1. Starting with the 1d energy equations (for \(x\) and \(\dot{x}\)) for an SHO; derive the equations of motion. Did you get the sign right?

#Canonical Coupled Oscillators#

Let’s assume you have a chain of two mass connected by springs (all the same \(k\)) as below.

Coupled Oscillator set up. Two oscillators connected by three springs in a horizontal line.

✅ Do this

  1. Write down the energy equations for this system (using \(x_1\) and \(x_2\) for coordinates)

  2. Write the Lagrangian and derive the two equations of motion.

  3. Do all the signs makes sense to you?

Choose your coordinates#

Coupled Pendulums#

Consider two vertical pendulums of length \(l\) connected via their masses \(M\) by a weak spring \(k\). By weak, we mean that the spring constant is small. See below for a canonical setup:

✅ Do this

  1. Write down the energy equations for this system (think about your choices of coordinates)

  2. Write the Lagrangian and derive the two equations of motion (we want to know what is happening with both bobs)

  3. Compare your work to another group. Did they choose the same coordinates?

Adding Constraint Forces#

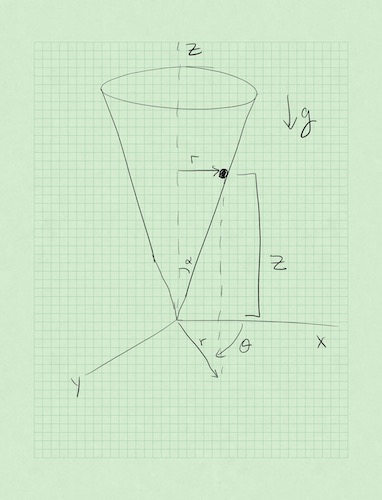
Rubric

Consider a particle of mass \(m\) constrained to move on the interior surface of a upside down smooth ice cream cone (aligned with the vertical axis) with half-angle \(\alpha\) subject to a gravitational force downward, so that the cone axis and gravity are aligned.

  1. Using cylindrical coordinates (why?), write down the equation of constraint. Think about where the mass must be if it’s stuck on a cone.

  2. Write the energy contributions in cylindrical coordinates. (This is where you put in the constraint!)

  3. Form the Lagrangian and find the equations of motion (there are two!)

## your code here