4 Oct 22 - Activity: Lagrangian Dynamics with Constraints#

One of the strengths of Lagrangian dynamics is that you do not have to have a mathematical description of the forces for all space and time. We can see that in this upside-down ice cream cone problem. How would you write the force of the cone for all space and time?

Answer: :shrugs:

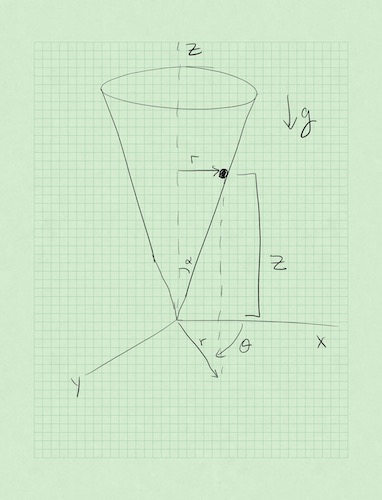
Rubric

Starting with Pencil and Paper Analytics#

Consider a particle of mass \(m\) constrained to move on the interior surface of a upside down smooth ice cream cone (aligned with the vertical axis) with half-angle \(\alpha\) subject to a gravitational force downward, so that the cone axis and gravity are aligned.

  1. Using cylindrical coordinates (why?), write down the equation of constraint. Think about where the mass must be if it’s stuck on a cone.

  2. Write the energy contributions in cylindrical coordinates. Do this in general first (use Cartesian and convert or start with cylindrical)

  3. Pop in the constraint equation. This reduces degrees of freedom (how do you see this?)

  4. Form the Lagrangian and find the equations of motion (there are two!)

Numerically analyze this system#

As a group, perform an analysis of this system (along the lines of what we have done in project 1). It is ok to split up tasks, but share the code and results!

Try to:

  • Create a phase space diagram

  • Characterize different motion

  • Numerically integrate the system

  • New to you: Investigate the energy over time

  • Challenging: Investigate the z-component of the angular momentum over time

## Your code here

Extend your analysis#

Now allow the bead to roll without slipping inside the cone. How does this change the energy? The equations of constraint?

  1. Write the energy equations for this new system.

  2. Write the equations of constraint for this system.