Homework 7 (Due. Mar 16)
1. Energy conservation
Consider an infinitely long solenoid of radius $a$ that is at the center of a large resistive ring (turns per length $n$; radius $b$; resistance $R$), here $b \gg a$. The current in the solenoid varies with time, $I_s(t)$, such that an electric field is created everywhere in space and thus a current is driven in the wire. In this problem, you will show that the power dissipated in the resistive wire is equal to the integral of the Poynting vector over the outside surface of the solenoid.
- In our discussion of energy conservation, $(\dfrac{dU_{mech}}{dt} + \dfrac{dU_{em}}{dt} = - \iint \mathbf{S} \cdot d\mathbf{A})$, we found we needed to pick a system. What system is appropriate to choose when considering the power dissipatedin the resistive wire? What does that tell you about the energy trasnported by the surroundings? That is, what is transporting energy into the resistive wire?
- There is a nonzero $\mathbf{S}$ as there is energy dissipated in the wire. What are the relevant electric and magnetic fields that contribute to this nonzero $\mathbf{S}$? Determine the direction of $\mathbf{S}$ in this case.
- By considering the limit of a very small radius solenoid, show that the magnitude of the power transported across the boundary of a cylinder encapsulating the solenoid is $(\pi \mu_0a^2 n\dfrac{dI_s}{dt})I_r$ where $I_r$ is the current in the resistive ring.
- Show that the result above is equal to the power dissipated in the resistive wire. How does this result fit with our statement of energy conservation, $(\dfrac{dU_{mech}}{dt} + \dfrac{dU_{em}}{dt} = - \iint \mathbf{S} \cdot d\mathbf{A})$?
2. Slowly accumulating charge
Consider a volume current that is (very slowly) flowing towards the $z$-axis,
Charge begins to accumulate along the $z$-axis.
- Find an expression for the accumulating charge as a function of time.
- Determine the electric field at a distance $s$ from the $z$-axis as a function of time in all of space.
- Determine the magnetic field in all of space due to the volume current and the accumulating charge.
- Discuss your results in the context of conservation of energy. Which aspects of the energy are increasing/decreasing? What are you defining as the region of interest?
3. Charging Capacitor
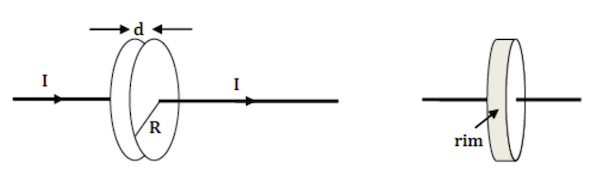
A capacitor with circular plates of radius $R$ separated by distance $d \ll R$ is being charged by a steady current $I$. The plates are sufficiently close that fringe effects can be ignored.
- Compute the magnitude of the B-field between the plates at all distances $r$ from the center of the plates ($r < R$ & $r > R$). Sketch the magnitude of the B-field vs. $R$.
- Compute the Poynting vector $\mathbf{S}$ (magnitude and direction) on the rim of the capacitor, between the plates, at $r = R$. (The “rim” is the ribbon of area at $r = R$ between the plates; see the diagram.)
- Show that the rate at which the capacitor’s stored energy is increasing $dU/ dt$ is equal to the rate at which field energy is entering through the rim: $\iint \mathbf{S}\cdot d\mathbf{A}$.
4. Poynting Vector of a Solenoid
Consider a very long solenoid of length $L$, radius $r$, and turns per length $n$. The current $I$ in the solenoid is linearly ramped from $I=0$ to $I=I_0$ over a period $t_0$ as shown in the graph.
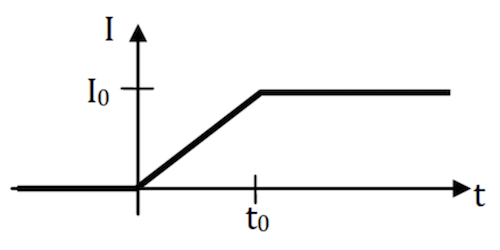
- Integrate the magnetic field energy density to derive a formula for the total field energy stored in the solenoid at times $t > t_0$.
- Solve for the electric field everywhere at times $0 < t < t_0$.
- Solve for the Poynting vector $\mathbf{S}$ (direction and magnitude) at $r = R$ (just inside the walls of the solenoid) as a function of time $t$.
- Show that the total field energy/time passing from the walls of the solenoid into its interior, when integrated from $t = 0$ to $t = t_0$, gives the same total energy as you computed in part 1.
5. Energy flow in a coax
We now want to investigate energy flow in a cylindrical coax cable. For now, let’s just look at fields constant in time, not varying in time. Assume that constant current $I$ flows in the $+z$ direction on the inner wire and that total current $I$ flows in the opposite direction in the shell. Also assume that there is a constant voltage difference $V$ between the wire and the shell, as shown.

- For this steady current and voltage case: Find $\mathbf{E}$ and $\mathbf{B}$ everywhere in space. You may assume that the coax cable (wire plus shell) is neutral.
- Calculate the Poynting vector $\mathbf{S}$ everywhere.
- The magnitude of $\mathbf{S}$ gives the energy flux density and represents the power per area moving through space. Does its direction make sense for the coax?
- Integrate this flux through the cross sectional area of the coax to find the power transported down the coax line. Does your answer make sense relative to the circuit maintaining the current and voltage? Briefly comment!
6. Paired Project Problem - Starting your pair project
This second project can (but doesn’t have to) build on the project you just complted. It is a team project that you will complete with a partner. This project is meant to mimic the common practice of poster preparation and presentation. In a nutshell, you will conduct an original modeling project where you analytically and computationally model some E&M phenomenon of your choosing, prepare a poster of the project, and present it to your classmates and me. In working on this project, you will be trying to answer the following questions:
- What is the area of E&M that you are doing research on?
- What are the questions that you are trying to answer about this area?
- What theoretical models can be used to answer those questions?
- What analytical and computational work did you do to answer those questions?
- What were the resulting predictions that your work produced?
- What are the limitations of what you have done? * What are some remaining open questions?
- What did each member of your pair contribute?
There will be six homework problems to help scaffold your work and poster development. In this first homework problem, you and your partner will write up a single document that answers the following questions:
- Who are the partners in this team?
- What are you and your partner proposing to do?
- What area of E&M will you be conducting original calculations for?
- What source material are you drawing from?
- What has been done so far and what are you going to do? It’s ok if it’s a solved problem, but you will need to reproduce what has been done and extend it beyond what your reference material offers.
As usual, you will turn in this document using GitHub.