Homework 11 (Due. Apr 13)
There are three physics problems this week, but the first two are quite similar…
1. Spring constant of an atom
In class we have modeled an atom as an electron with mass $m$ attached to the heavy nucleus with a spring. This atomic spring has zero equilibrium length and spring constant $k = m\omega_0$. Here we show that this model, though crude, is not crazy. Quantum mechanics tells us that in the ground state of hydrogen, the electron wave function is a spherically-symmetric cloud of charge centered on the atom. So, without too much violence to reality, we can model the electron as a uniform sphere of charge of radius $R$ = Bohr radius = 0.53 angstroms). When an external E-field is applied, the nucleus is pushed one way and the electron cloud is pushed the other way, so there is an induced dipole moment. We assume that the electron’s sphere of negative charge is not distorted in shape when it is displaced. We also assume that the nucleus is so heavy that it remains stationary, while the electron cloud can oscillate about the stationary nucleus.
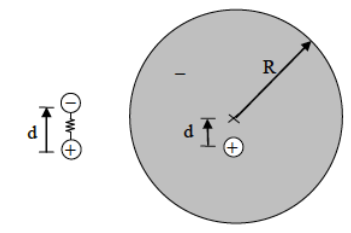
- Show that when the nucleus is displaced from the center of the electron cloud by a distance $d < R$), there is a restoring force that is proportional to $d$. Derive an expression the spring constant $k$ in this situation.
- Compute the value of the spring constant $k$, for the case of a hydrogen atom. Give the answer in both SI units (N/m = J/m$^2$) and in slightly more natural units of electron-volts per angstrom$^2$ (eV/Å$^2$). What is the natural frequency $f_0 = ω_0/2\pi$ (in Hz) for this mass-spring system?
- What is the wavelength of light that has this frequency? (Give your answer in nanometers.) What part of the spectrum does this correspond to? (Visible?, IR?, UV?, radio?, etc…)
2. Dispersion in hydrogen gas
When we first studied polarization in matter, we used a very simple atomic model to estimate the atomic polarizability from a static electric field. Now let’s apply it for non-static fields.
- Assume the hydrogen atom is a point nucleus of charge $+e$ and mass $m_p$ surrounded by a sphere of uniform charge density of radius $r_H$ and total charge $-e$. In the absence of any external field, the equilibrium position of the nucleus is at the center of sphere. Find the force on the nucleus if it is displaced from the center by a distance d and use this to find an “effective” spring constant k. What is the natural frequency of oscillation for the hydrogen atom in this model? Putting in the actual values for the variables (the radius will be approximate of course), where in the electromagnetic spectrum does this frequency lie? (Hint: think about what you can reuse from question 1)
- For EM waves with frequencies far from the region of anomalous dispersion, we can ignore damping and use: $n=1 + \left(\dfrac{Nq^2}{2m\varepsilon_0}\sum_j\dfrac{f_j}{\omega^2_j}\right)+\omega^2\left(\dfrac{Nq^2}{2m\varepsilon_0}\sum_j\dfrac{f_j}{\omega^4_j}\right)$ or $n=1+A(1+B/\lambda^2)$ in terms of the wavelength, to predict the coefficients of refraction and dispersion for hydrogen. Use the numbers from part (a), and calculate these coefficients for hydrogen gas at STP, and compare them to the measured values of $A=1.36\times10^{-4}$ and $B=7.7\times10^{-15}$m$^2$.
3. Waves in plasmas
Consider a neutral plasma (gas of electrons and positive ions), with electron density $N_e$. At high frequencies, because the ions are very heavy, we can consider them to be essentially fixed and any current due solely to the light electrons. The total charge density can be set to zero for an electrically neutral gas.
- Use Maxwell’s Equations to derive the wave equation for the electric field: $\nabla^2 \mathbf{E} -\dfrac{1}{c^2}\dfrac{\partial^2}{\partial t^2}\mathbf{E} = \mu_0 \dfrac{\partial}{\partial t}\mathbf{J}$
- For a monochromatic wave, $\mathbf{E} = Re(\widetilde{\mathbf{E}} e^{−i\omega t})$, and ignoring any collision between electrons (mass $m_e$), use Newton’s law to relate $\mathbf{E}$ and $\mathbf{J}$ and show that $\left(\nabla^2 + \dfrac{\omega^2}{c^2}\right)\widetilde{\mathbf{E}} = \dfrac{\omega_p^2}{c^2}\widetilde{\mathbf{E}}$ where $\omega_p^2 = \dfrac{N_e e^2}{\varepsilon_0 m_e}$ is the plasma frequency.
- Derive the dispersion relation $k=\sqrt{\omega^2-\omega_p^2}/c$. Sketch the graph of $\omega(k)$.
- Give the real elecrtic field when $\omega < \omega_p$.
4. Project Problem - Draft figures and captions
Make sure to read the feedback that you received on your figure/models and think about how you and your partner are going to work through these details.
At this point, you should produce draft figures for poster with captions. You should have pressed onward with your calculations and produced appropriate figures for your poster with captions. The “graphic” and caption should be turned in. These need not be complete in the sense that you should continue working on your calculations and models until the poster is turned in. By draft, I do mean draft, so any figures that you are thinking about putting in the poster, please include them in their current form. Make sure to give me enough information to:
- judge what the figures are,
- where they will go in the poster, and
- what part of the poster story they will be telling.
In addition, please continue to reflect on:
- Who did what?
- What questions were you able to answer last week?
- What questions do you need to answer to continue to move forward?
- What help do you need from me or others?
You will turn in both your “notebook” and your self-reflection using the same GitHub repository you started for Project 2. Make sure that you sync your repository first to get the new feedback!