There are fewer homework problems and no computational problem this week, so you can focus on the project problem (Problem 5 below). It is very important to work on the project problem this week because it starts you on the process of writing your paper. The project problem will take you longer than it has in the past, so start early!

1. Time varying magnetic field

A conducting disk with radius $a$, height $h \ll a$, and conductivity $\sigma$ is immersed in a time varying but spatially uniform magnetic field parallel to its axis:

$$\mathbf{B} = B_0 \sin(\omega t)\hat{\mathbf{z}}$$

1. Ignoring the effects of any induced magnetic fields, find the induced electric field $\mathbf{E}(\mathbf{r},t)$ and current density $\mathbf{J}(\mathbf{r},t)$ in the disk. Sketch the current distribution.
2. Compare $\mathbf{E}(\mathbf{r},t)$ to the electric field in presented in problem 1 on Homework 2 when $\omega t \ll 1$.

2. Conducting “tethers” in space

Tethers can use the velocity of a spacecraft through the Earth’s magnetic field to generate electrical power. Alternatively, electrical currents pushed through the tether might be used to change the spacecraft velocity for either propulsion or for braking and reentry. Several ‘space tether’ experiments have been flown, to investigate the possible use if Faraday’s law for power generation and/or propulsion. Examples are the 1996 joint US/Italy effort to deploy a 20 km tether from one of the space shuttles to generate power, or the European Space Agency’s Young Engineers Satellites (YES2) experiment that deployed a 31 km tether as a means of reentry for a small payload dropped from a Russian Foton spacecraft.

1. What is a typical low-Earth orbital velocity? To be definite, assume an orbit 200 miles above the surface of the Earth. Assuming that you increase the velocity, do you go to a higher or lower orbital altitude?
2. The Earth has a magnetic field that is approximately described by an ideal magnetic dipole. This field apparently arises from circulating charge currents within the convective parts of the Earth’s mantle. These flows are directly related to the flows causing plate tectonics. Fascinating stuff… OK, so look up a typical size of the Earth’s magnetic field at some location on the Earth’s surface, use it along with the dipole field model to estimate the Earth’s magnetic dipole moment magnitude, m. Using some information about the size of the Earth’s core, mantle, etc. Estimate the electric current that must be flowing to produce this magnetic moment.
3. Now combine the typical orbital velocity and the typical magnetic field magnitude and direction to calculate the motional EMF that could be generated along a 20 km conductive cable. Assuming the orbit is around the magnetic equator, in which direction relative to the orbital velocity direction would you deploy the cable to create the largest EMF?
4. Lovely, so now you have a cable stretched out and it has some EMF generated along its length. However, to generate useful POWER, the product of current and voltage, you need to have a closed circuit to allow current to flow. Perhaps you could stretch a second cable out from your spacecraft to touch the first cable and to complete the circuit? Explain why that’s not going to work.
5. In fact, the circuit is completed by the ionized plasma that surrounds the Earth, the so-called ionosphere. In the shuttle tether, there was an insulating, roughly 1cm diameter nylon cable surrounded by conductive copper braid of 3 mm thickness, all wrapped in an insulating Kevlar layer. Data taken during the experiment suggested that the ionosphere was ‘somewhat less conductive’ than the copper braid. Make life simple by assuming that the ionosphere conducted in a cylindrical pipe 20 km long and with cross sectional area equal to the areal size of the space shuttle (roughly 200 square meters) estimate the plasma conductivity. What additional information would you need to know to estimate the density of charged particles in the plasma?

3. Mutual Inductance

We have an infinitely tall solenoid (radius $R$, $n$ coils per unit length). Wrapped around it is a single loop of wire (radius $r$, centered at the left edge of the solenoid, shown below).

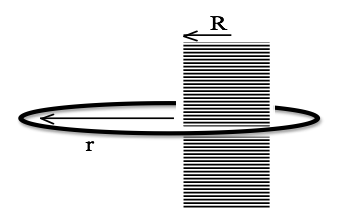
1. Find the mutual inductance $M$ between the loop and the solenoid. Would it be bigger, smaller, or the same, if $r$ was twice as big?
2. Suppose now that the loop is doubled up, so (with the same radius $r$) it wraps around the solenoid twice. Again, find the mutual inductance $M$.
3. If the solenoid was not infinitely long, would the mutual inductance between the solenoid and the single loop get larger or smaller? Briefly (qualitatively only) why?
4. Find the self-inductance per unit length of the infinite solenoid, all by itself. Explicitly check that the units of your answer work out correctly.

4. More mutual inductance

Two circular loops of wire are arranged so that they lie in the same plane and are concentric. One loop, of radius $a$, is TINY, much smaller than the other, which has radius $b$, i.e. $a«b$.

1. If the small loop is driven with a time varying current $I(t)$, derive an approximate formula for the induced EMF in the large loop. State the approximations or assumptions you make in your derivation.

5. Project Problem - Building your paper I

Last week, you completed your summary of two more papers. At this point, you should have read and summarized at least 4 papers describing the phenomenon that you are interested in. You should have also developed a sense of what resources you need to further understand the phenomenon that you are investigating in this paper.

To help you start building your paper, this homework problem asks you to summarize your background research so far. I am looking for about 4-5 paragraphs on what you have learned so far with references. Think about writing this as part of your eventual paper, so work to write something that is coherent and tells a complete story. Make sure you check it for spelling and grammar. This is your chance to make headway on the eventual project that you will turn in soon.

In writing this think about:

• What are people saying about this phenomenon? Is there agreement about how it is explained?
• What are the relevant models? How are the models described?
• How do people investigate it theoretically? Experimentally? Computationally?
• What are open questions surrounding the phenomenon?

You will turn this in using your GitHub repository.