Homework 1 (Due. Jan 19)
1. Sketching
- Make a quick sketch, in the x-y plane, of the following (two-dimensional) vector function. Plot enough different vectors to give a feeling for what this field looks like in the x-y plane.
- Explain briefly in words what this plot is showing. Is it physically realizable as an electrostatic field?
- Do the same as above for the field: (Here, I am assuming we are in 3-D spherical coordinates, but there is no azimuthal dependence. How should you “sketch” this?) Where have you seen this field before?
2. Divergence and Curl of a Vector Field
For each of the vector fields sketched below:
- Which of them have nonzero divergence somewhere? If the divergence is nonzero only at isolated points, which point(s) would that be?
- Which of the following fields have nonzero curl somewhere? If the curl is nonzero only at isolated points, which point(s) would that be?
A. 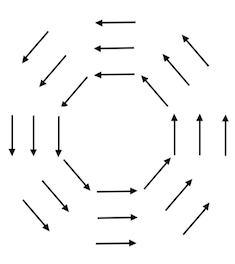
(Note: All arrows are the same length)
B. 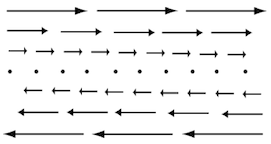
(Note: Arrows have no length in the middle)
C. 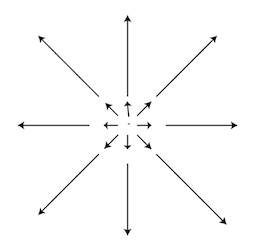
(Note: Arrows growing in length as $r^2$)
D. 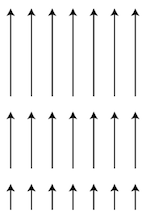
E. 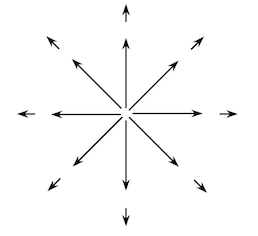
(Note: Arrows decreasing in length as $1/r^2$. Think of a “Coulomb field” of a point charge here…)
3. A few short computations
- Compute the divergence and curl of $(x+y)\hat{\mathbf{i}}+(y+z)\hat{\mathbf{j}}+(x-2z)\hat{\mathbf{k}}$.
- Could this field be a physical electrostatic field in some limited region of space near the origin? Very briefly, explain your reasoning.
- Given the following mathematical form for a volume charge density $\rho(\mathbf{r})$, describe the charge distribution in words, and also draw a little sketch showing where the charges are: $\rho(\mathbf{r}) = a\delta^3(\mathbf{r}-\mathbf{R}) + b\delta(r-R)$, where $a$, $b$ are given constants with appropriate units, $\mathbf{R}=\langle 2,0,0\rangle$, and as usual $r = \lvert\mathbf{r}\rvert$.
- What are the (SI metric) units of $a$ and $b$ in the charge density expression above?
- What is the total charge, in terms of the given constants in the equation?
4. The Electric Field and Gauss’ Law
- What exactly is $\mathbf{E}$, the electric field? Define it. How do you think about it, both mathematically and in words. Please define any technical words you introduce.
- Gauss’ Law states: $\oint_S \mathbf{E}\cdot\hat{\mathbf{n}}\,dA = \frac{q_{enclosed}}{\varepsilon_0}$ Suppose I evenly fill a cube (length $L$ on a side) with electric charge. I then imagine a larger, closed cubical surface neatly surrounding this cube (length $2L$ on a side). Can you use Gauss’ law (above) to simply compute the value of the electric field at arbitrary points outside the charged cube? (Don’t try, just tell me if you could, and why/why not?)
5. Field, Charge, and Voltage
Given that an electric field in some region of space is given by $\mathbf{E}(x,y,z) = cy\hat{\mathbf{j}}$, where $c$ is a given constant.
- What are the SI units of c?
- What, if anything, can you tell us about the charge density throughout this region, $\rho(x,y,z)$?
- What is the voltage associated with this E field? (Is your answer unique?)
6. The Magnetic Field
You have an infinitely tall, infinitesimally thin cylindrical sheet of surface current running around the $z$-axis, i.e., $\mathbf{K} = K_0 \hat{\phi}$ at $s=R$ (otherwise 0), as shown below.
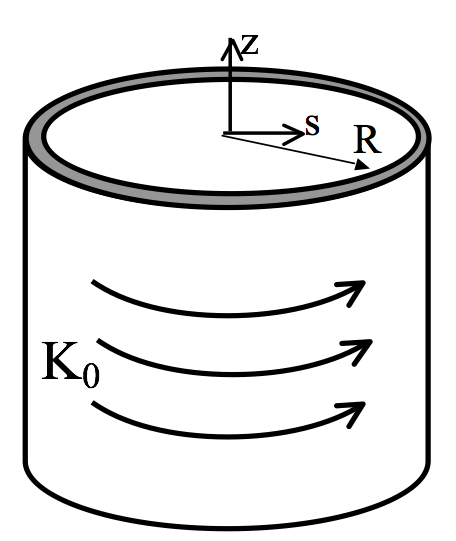
- What are the SI units of $K_0$?
- Sketch the magnitude of the resulting $B$ field as a function of radial distance, $s$ (both inside and outside the sheet).
- Briefly, show/explain your work for part 2. (If you grabbed a formula from Griffiths, explain concisely where it comes from.)
7. Plotting The Electric Field
In this problem, use a Jupyter notebook to plot the field of:
- a positive point charge
- an electric dipole
- an electric quadrupole
You might want to review homework sets from PHY 481 or just look up how to use quiver plot with Matplotlib.
You will turn this in using a GitHub repository. Please see Piazza for more instructions.
8. Project Problem - What is interesting?
This problem is to help you get started on your individual research project. First, define your phenomenon: what is it and why is it interesting to you? Find a few papers (at least 4) that you can use to start your background research. Please give the full references to these papers. Write 2 to 3 paragraphs that describe your phenomenon and your interest in it.
You will turn this in using a GitHub repository. Please see Piazza for more instructions.