Homework 12 (Due. Apr 20)

1. Star Wars with relativity

Space Probe #1 passes very close to earth at a time that both we (on earth) and the onboard computer on Probe 1 decide to call t = 0 in our respective frames. The probe moves at a constant speed of 0.5$c$ away from earth. When the clock aboard Probe 1 reads t = 60sec, it sends a light signal straight back to earth.

1. At what time was the signal sent, according to the earth’s rest frame?
2. At what time in the earth’s rest frame do we receive the signal?
3. At what time in Probe 1’s rest frame does the signal reach earth?
4. Space Probe #2 passes very close to earth at t = 1sec (earth time), chasing Probe 1. Probe 2 is only moving at 0.3c (as viewed by us). Probe 2 launches a proton beam (which moves at v = 0.21c relative to Probe 2) directed at Probe 1. Does this proton beam strike Probe 1? Please answer twice, once ignoring relativity theory, and then again using Einstein!

2. Muon calculations

The mean lifetime of muons is 2 $\mu\text{s}$ in their rest frame. Muons are produced in the upper atmosphere, as cosmic-ray secondaries.

1. Calculate the mean distance traveled by muons with speed $v = 0.99c$, assuming classical physics (i.e. without special relativity).
2. Under this assumption, what percentage of muons produced at an altitude of 10 km reach the ground, assuming they travel downward at $v = 0.99c$? Careful here, you will have to think about the distribution of lifetimes given that particle decay is a Poisson process.
3. Calculate the mean distance traveled by muons with speed $v = 0.99c$, taking into account special relativity.
4. Under this assumption, what percentage of muons produced at an altitude of 10 km reach the ground, assuming they travel downward at $v = 0.99c$?

3. $\pi$ Mesons

A group of $\pi$ mesons (pions) are observed to be traveling at $u’ = 0.8c$ in a physics laboratory. The mean lifetime (let’s call it $\lambda$ ) for unstable particles undergoing exponential decay is the average time for a group of particles to be reduced to $1/e$ of their original number. We can express this mathematically as: $N_t = N_0 exp(−\Delta t / \lambda)$. We see then that for $\Delta t = \lambda$ , $N_t = N_0 exp(−1) = (1 / e) ⋅ N_0$

1. What is the $\gamma$–factor for these pions?
2. If the pions’ proper mean lifetime is $\lambda$ = 2.6 × 10$^{−8}$ s, what is the lifetime ($\lambda’$) as observed in the laboratory frame?
3. If there were initially 32,000 pions, how many will be left after they have traveled 36 meters, from the source to a detector (as measured in the laboratory frame)?
4. Show that this number is the same, as calculated in the rest frame of the pions. Explain this calculation.
5. What would the answer to part 4 be if there were no time dilation (i.e., $\Delta \tau = \Delta t’$)?
6. How long does the distance of 36 meters in the laboratory frame appear to the pions in their rest frame?
7. Use the result from part 6 and the proper time elapsed (as calculated in the rest frame of the pions) to find the velocity of the laboratory frame, as calculated in the rest frame of the pions.

4. Dealing with simultaneity and observations

It is important to understand that the effects of special relativity are in no way due to the fact that light travels at a finite speed, but rather due to the fact that the speed of light is the same finite quantity in any inertial reference frame. We can always take into account the time it takes for light to travel some distance, and in fact, we must do so in order to ensure that all the local clocks at rest relative to each other in our frame of reference are properly synchronized. The goal of this problem is to understand the difference between what a single observer perceives (with her eyes), and what a system of local observations made with synchronized clocks will record. The main issue is that a single observer can only perceive information that has actually had time to reach her. This means the one observer is only going to see things as they arrive, usually delayed by the speed of light from where the events actually happened. Things that happened farther away, but at earlier times, will be arriving at the location of a single observer at the same time. Consider a rod of proper length $l_0$ , moving at speed $v$, relative to frame S. Careful measurements made by local observers in S will show that the rod has the contracted length: $l = l_0/\gamma$.

But now consider what is seen by a single Observer Q:

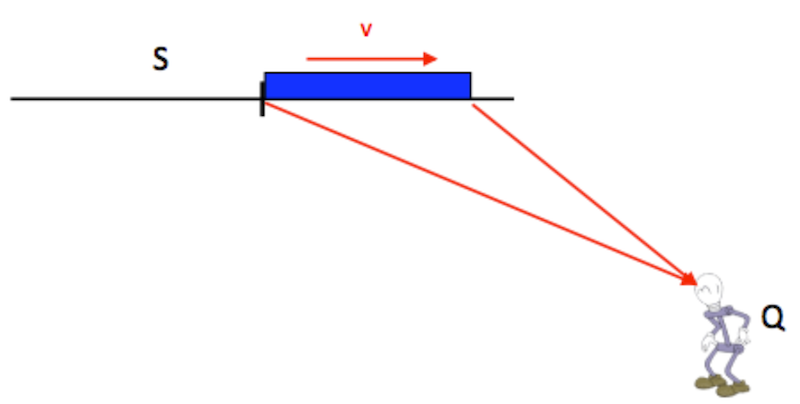
What Observer Q sees at any one instant is determined by the light entering her eyes at that instant. Now, consider the light reaching Observer Q at one instant from the front and back ends of the rod.

1. Explain in words why these two light rays must have left the two ends of the rod at different times.
2. Prove that Observer Q sees a rod that is longer than $l$. (In fact, at certain speeds, it is even seen to be longer than $l_0$, and the length contraction is actually perceived as an expansion.)
3. Prove that once it has passed her (the rod is now to the right of her), Observer Q will now see the rod to be shorter than $l$.
4. Explain how your analysis in parts 1-3 relates to synchronized clocks, simultaneity, and making an observation (in physics).

5. Project problem - Choose your feedback

You’ve been working on this project for a while now and this will be the last formal project problem. Think about what feedback you want from me regarding your project. What would be helpful? What do you need some direction or instructions on? Think about what would help you the most to make a successful poster in a couple of weeks. Write up a short document outlining what feedback you feel that you need and direct me to the document(s) to review.

This kind of work models what your advisor (or boss) might do when you are presenting a project that you’ve been working on. You know the details of the project better than the advisor (or boss), but you might still want help thinking about the big picture or, perhaps, some specific details that you want to check.

As usual, commit these changes to your repository.