Homework 13 (Due. Apr 27)

1. Magnetic field of a wire

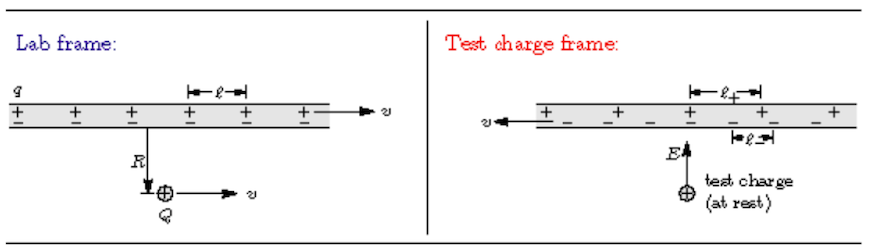
Shown above is a model of a wire with a current flowing to the right. To avoid minus signs we take the current to consist of a flow of positive charge carriers, each with charge $+q$, separated by an average distance of $l$. The wire is electrically neutral in the lab frame, so there must also be a bunch of negative charges, at rest, separated by the same average distance $l$ in this frame. Be aware that charge is Lorenz invariant: a charge Q has the same value in every inertial frame.

1. Using Gauss’ law, what is the electric field outside this wire in the lab frame? Suppose there is a test charge $+Q$ outside the wire, a distance $R$ from the center of the wire, moving to the right (For simplicity, let’s say the velocity is the same as that of the moving charges in the wire, i.e. $v$, as shown in the figure.)
2. Given your answer for the E-field, what is the electrostatic force on this charge, in this frame?
3. Using Ampere’s (and the Lorentz force) law - what is the magnetic force on the moving test charge $Q$?
4. Put it together, what is the magnitude and direction of the net force on the test charge, and what “causes” it?
5. Now consider how all this looks in the reference frame of the test charge, where it’s at rest. In THIS frame, what is the magnetic force on the test charge $Q$? In this frame, it’s the negative charges in the wire that are moving to the left. Because they’re moving, the average distance between them is length-contracted. Meanwhile the positive charges are now at rest, so the average distance between them is now longer than $l$.
6. What is the average distance ($l_+$) between the positive charge carriers in this frame? Both of these effects give the wire a non-zero charge density.
7. Compute the charge density (charge per length) in this frame, with the correct overall sign.
8. Use Gauss’s Law to compute the electrostatic force on the test charge.
9. In THIS frame, what is the magnitude and direction of the force on the test charge, and what “causes” it?
10. For normal currents, $\beta = v/c$ is about $10^{−13}$. (Drift velocities are small!) Given this, show that the forces you computed in parts 4 and 9 are the same size. Hint: expand in a Taylor series.

2. E&B transformations

$$\bar{E}_{x} = E_{x} \qquad \bar{E}_y = \gamma\left(E_y-vB_z\right) \qquad \bar{E}_z = \gamma\left(E_z+vB_y\right)$$ $$\bar{B}_{x} = B_{x} \qquad \bar{B}_y = \gamma\left(B_y+\dfrac{v}{c^2}E_z\right) \qquad \bar{B}_z = \gamma\left(B_z-\dfrac{v}{c^2}E_y\right)$$

1. Use these equations to show that both $\mathbf{E}\cdot\mathbf{B}$ and $(E^2 − c^2 B^2)$ are Lorentz invariants.
2. We found earlier that $\mathbf{E}$ and $\mathbf{B}$ are mutually perpendicular for traveling EM waves. Given that this is true in some frame, can there be any other reference frame in which you would find $\mathbf{E}$ and $\mathbf{B}$ not perpendicular for traveling EM waves?
3. Suppose $E > cB$ in some frame. Show that there is no possible frame in which $E=0$.
   • If $E = 0$ in some frame, do these relations mean that $E$ is always equal to 0 in every other inertial frame?
   • If $B = 0$ (but $E$ is nonzero) in some frame, can you always (ever?) find another frame in which $E = 0$ (but $B$ is nonzero)?

3. Maxwell’s equations written compactly

We found that we could write the field tensor like this

$$F^{\mu\nu}=\left( \begin{array}{cccc} 0 & E_x/c & E_y/c & E_z/c\\ -E_x/c & 0 & B_z & -B_y\\ -E_y/c & -B_z & 0 & B_x\\ -E_z/c & B_y & -B_x & 0\\ \end{array} \right)$$

and the dual tensor like this,

$$G^{\mu\nu}=\left( \begin{array}{cccc} 0 & B_x & B_y & B_z\\ -B_x & 0 & -E_z/c & E_y/c\\ -B_y & E_z/c & 0 & -E_x/c\\ -B_z & -E_y/c & E_x/c & 0\\ \end{array} \right)$$

With the current density 4-vector written as this: $J^{\mu} = (c\rho,J_x,J_y,J_z)$, we claim that Maxwell’s equations in vaccuum are given thusly,

$$\dfrac{\partial F^{\mu\nu}}{\partial x^{\nu}} = \mu_0 J^{\mu}, \qquad \dfrac{\partial G^{\mu\nu}}{\partial x^{\nu}} = 0$$

1. Show by explicit calculation that you can recover all 4 Maxwell’s equations.
2. What would have happened if $\dfrac{\partial G^{\mu\nu}}{\partial x^{\nu}} \neq 0$? Think about what happens physically?! It must be zero!

Self-Reflection (PHY 481 and 482)

We’ve talked about a lot of different things in E&M 1 and 2. In doing so, we’ve covered Chapters 1-9 and 12 of Griffiths along with a bunch of other special topics. You’ve studied systems on your own and learned a ton of E&M. Think about where your E&M knowledge was at the beginning of last fall and where it is now.

1. Write up a half-page or so about how you feel your understanding of E&M has changed. Think about what you enjoyed learning most, what you felt you learned most deeply, and what you think that means for you in your future as a physicist.
2. On the first day of class in PHY 481, I asked you to draw a concept map of E&M. How different concepts were connected and why they were connected that way. Draw another one now. Think about all the new knowledge you have gained and how it all fits together. Focus on the high level concepts and ideas and fill in as much detail as you feel you need to make your point.