Homework 6 (Due October 11th)
Homework 6 emphasizes the conductor problem, which requires new methods to approach finding $V$ or $\mathbf{E}$ as we are often unable to find $\rho$ a priori. In the presense of an external electric field, charges will shift in a conductor, thus complicating matters of finding $\rho$.
1. Assessment is on-going
TURN THIS WORK IN SEPARATE FROM YOUR REGULAR HOMEWORK TO DANNY
An examination is one measure of your understanding at a given moment in time. It is often a stressful and high stakes situation, which means that folks tend to perform differently depending on how this situation affects them. My goal is not for you to perform physics (i.e., just get the right answer), but to become reflective of your learning of physics (and of learning in general). To that end, I would like to invite you to re-solve the first exam. I’ve posted a PDF here.
In addition to solving the problems again, I would like you to write a short summary of what you felt like you did incorrectly at the time of the exam for each problem (i.e., what you think you got wrong and why) and how your solution resolves this problem (i.e., what approach you needed to take to solve the problem correctly). What I’m asking is that you reflect on your exam solutions and what understanding you needed to draw on to solve the problems.
You are welcome to work on the problems together, but your reflection should be your own and individualized. It is through this kind of thinking about our own learning that we become expert learners.
Completing this exercise will not count towards your homework, but will instead reward you with earning 1/2 of the (non-bonus) credit back on your exam.
2. GRE Prep: Concentric condcuting shells
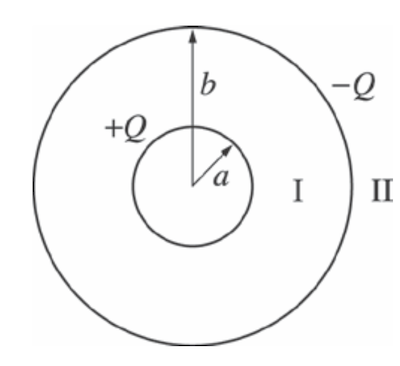
Two thin, concentric, spherical conducting shells are arranged as shown in the figure above. The inner shell has radius $a$, charge $+Q$, and is at zero electric potential. The outer shell has radius $b$ and charge $-Q$.
- If $r$ is the radial distance from the center of the spheres, what is the electric potential in region I ($a<r<b$) and Region II ($r > b$)?
- Region I: $\dfrac{Q}{4\pi\varepsilon_0}\frac{1}{r}$; Region II: 0
- Region I: $\dfrac{Q}{4\pi\varepsilon_0}\left(\frac{1}{r}-\frac{1}{a}\right)$; Region II: 0
- Region I: $\dfrac{Q}{4\pi\varepsilon_0}\left(\frac{1}{r}-\frac{1}{b}\right)$; Region II: $-\dfrac{Q}{4\pi\varepsilon_0}\frac{1}{r}$
- Region I: $\dfrac{Q}{4\pi\varepsilon_0}\left(\frac{1}{r}-\frac{1}{a}\right)$; Region II: $\dfrac{Q}{4\pi\varepsilon_0}\left(\frac{1}{b}-\frac{1}{a}\right)$
- Region I: $\dfrac{Q}{4\pi\varepsilon_0}\left(\frac{1}{r}-\frac{1}{b}\right)$; Region II: $\dfrac{Q}{4\pi\varepsilon_0}\left(\frac{1}{a}-\frac{1}{b}\right)$
- Explain how you determined your answer. Consider the charge, the potential, and the relevant electric field. You may demonstrate this with sketches if it helps. Explain any “shortcut” you used to eliminate possible answers.
3. Capacitors, metals, and continuity
We have discovered that there is a curious result when looking at the electric field across a boundary. It is discontinuous! by an amount that is consistently the same expression ($\sigma/\varepsilon_0$). However, we have also found that the electric potential across the boundary is continuous.
Consider a very large set of metal capacitor plates separated by a small distance $d$. Each plate is charged with an equal amount of charge, but the left plate is negative. So, the left plate carries $-\sigma$ and the right plate carries $+\sigma$.
- Find the electric field everywhere in space (consider that the plates extend to infinity to ignore any edge effects).
- Plot the component of the electric field along a line that runs to the plates.
- Find the electric potential everywhere in space. You are free to set where $V=0$, but be careful when doing so as the distribution of charge extends to infinity!
- Plot the electric potential along the same line as in Part 2.
- What do you notice about the graphs you sketched in Parts 2 and 4?
- BONUS: Consider that the plates have some depth to them (as with any real physical plate). Let them have a width $w$. Using what you remember or know about metals, what happens to your graphs in Parts 2 and 4? (For example, we will learn soon that metals in electrostatics are equipotential surfaces.)
4. Gauss’ Law and Cavities
A metal sphere of radius $R$, carrying a charge $+q$, is surrounded by a thick concentric metal shell (inner radius $a$, outer radius $b$). The shell carries no net charge. Where requested, please explain your reasoning.
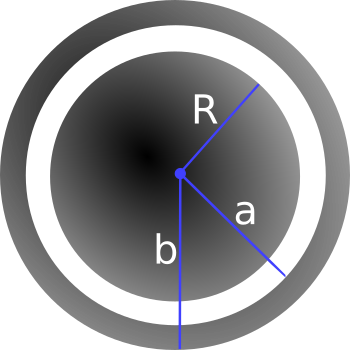
- Sketch the charge distribution everywhere. If the charge is zero anywhere, indicate that explicitly.
- From part 1, you probably noticed the charge distributes in some way on the metals. Determine the surface charge density $\sigma$ at $R$, at $a$, and at $b$.
- Sketch the electric field everywhere; explain how you know the field you have drawn is correct. If the field is zero anywhere, indicate that explicitly.
- Find the potential everywhere, use $r \rightarrow \infty$ as your reference point for $V=0$.
- Now the outer surface is touched by a grounding wire, which lowers its potential to zero. How do your answers change to parts 2 and 4? Explain your reasoning.
5. Coax capacitors
Consider a coaxial cable with an inner conducting cylinder has radius $a$ and the outer conducting cylindrical shell has inner radius $b$. It is physically easy to set up any fixed potential difference $\Delta V$ between the inner and outer conductors. In practice, the cable is always electrically neutral.
- Assuming charge per length $+\lambda$ and $-\lambda$ on the inner and outer cylinders, derive a formula for the voltage difference $\Delta V$ between the cylinders.
- Assuming infinitely long cylinders, find the energy stored per length (W/L) inside this capacitor. Notice we are asking for the energy per unit length, the answer is not infinity! Let’s do it two ways so we can check:
- Find the capacitance per length ($C/L$) of this system, and then use stored energy $W = \frac{1}{2} C (\Delta V)^2$.
- Integrate the energy density stored in the E field.
- Based on your answers to part 2, where in space would you say this energy is physically stored?
- Estimate the capacitance per meter of the coaxial cable that the cable company uses to send TV signals into homes. Justify any assumptions.
- This model is also excellent for “axons”, which are long cylindrical cells (basically coax cables) carrying nerve impulses in your body and brain. Estimate the capacitance (in SI metric units, Farads) of your sciatic nerve. Assumptions - the sciatic nerve is the longest in your body, it has a diameter of roughly 1 micron, and a length of perhaps 1 m. Note that axons generally have a value of b which is very close to a (i.e. the gap is extremely tiny, b-a is about 1 nanometer. ) so you can simplify your expression using $ln(1+\epsilon)\approx\epsilon$.
6. Superposition in conductors (“shielding”)
We carve out two spherical cavities from a metal sphere of radius $R$ (as shown below). The first cavity (radius, $a$) has a charge $+q_a$ placed at the center of the cavity. Similarly, the second cavity (radius, $b$) has a charge $+q_b$ placed at the center of that cavity.
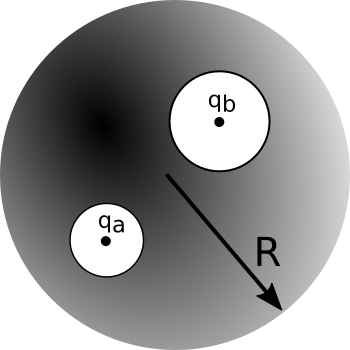
- Sketch the surface charge everywhere. Explain how you know the surface charge looks this way.
- Determine the surface charges ($\sigma_a$, $\sigma_b$, and $\sigma_R$).
- Sketch the electric field everywhere. If the field is zero anywhere, indicate this explicitly. Explain how you know the electric field looks this way.
- Determine the magnitude of electric field outside the conductor and inside each cavity.
- If we brought an external charge $q_c$ near the conducting sphere how do your answers to parts 1-4 change? You may answer in words, pictures or both.