Homework 12 (Due November 22nd)

Homework 12 focuses on computing the magnetic field using Biot-Savart and Ampere’s Law, which are the two direct methods for computing the magnetic field.

Dropbox link for HW 12

1. Magnetic field of distributed currents

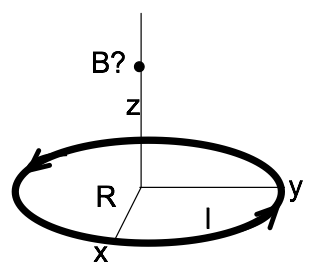
1. Compute the magnetic field $\mathbf{B}(0,0,z)$ along the $z$-axis for a current loop (current $I$, radius $R$, sitting in $x-y$ plane, centered around the $z$-axis). It is shown in the figure above.
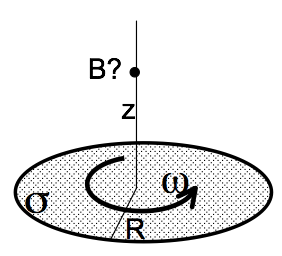
2. Last week we had a DVD (radius $R$) with a fixed, constant, uniform surface electric charge density $\sigma$ everywhere on its top surface (figure below). It was spinning at angular velocity $\omega$ about its center (the origin). You found the current density $\mathbf{K}$ at a distance $r$ from the center. Use that result to find the magnetic field $\mathbf{B}(0,0,z)$ at any distance $z$ directly above the origin. (Part 1 above might help.)
3. Does your answer to part 2 seem reasonable? Please check it, with units, and some limiting behaviors (e.g. what do you expect if $R \rightarrow 0$? $\omega \rightarrow 0$? $z\rightarrow \infty$? For this last one, don’t just say “it goes to zero. This is a dipole, so $B$ should go to 0 like $1/z^3$. (Right?) Show that it does!

2. Magnetic field of a bent wire

An infinitely long wire has been bent into a right angle turn, as shown. The “curvy part” where it bends is a perfect quarter circle, radius $R$. Point P is exactly at the center of that quarter circle. A steady current $I$ flows through this wire.

1. Find $\mathbf{B}$ at point P (magnitude and direction) (No need to derive any formulas “from scratch” if you can get them from Griffiths’ examples!)

3. Ampere’s Law - themes and variations

Consider a thin sheet with uniform surface current density.

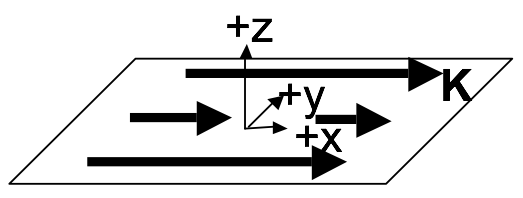
1. Use the Biot-Savart law to find $\mathbf{B}(x,y,z)$ both above and below the sheet, by integration. Note: The integral is slightly nasty. Before you turn to WolframAlpha - simplify as much as possible! Set up the integral, be explicit about what curly $R$ is, what $da’$ is, etc, what your integration limits are, etc. Then, make clear mathematical and/or physical arguments based on symmetry to convince yourself of the direction of the B field (both above and below the sheet), and to argue how $\mathbf{B}(x,y,z)$ depends (or doesn’t) on $x$ and $y$. (If you know it doesn’t depend on x or y, you could e.g. choose x=y=0 to simplify… But first you must convince us that’s legit!)
2. Now solve the above problem using Ampere’s law. (Much easier than part 1, isn’t it?) Please be explicit about what Amperian loop(s) you are drawing and why. What assumptions (or results from part 1) are you making/using? (Griffiths solves this problem, so don’t just copy him, work it out for yourself!)
3. Now let’s add a second parallel sheet at $z=+a$ with a current running the other way. (Formally, this means $\mathbf{J}=-K_0\delta(z-a)\hat{x}$. Do you understand this notation?) Use the superposition principle (do NOT start from scratch or use Ampere’s law again, this part should be relatively quick) to find B between the two sheets, and also outside (above or below) both sheets. Does this remind you of a familiar electrostatics problem at all? How?
4. Griffiths derives a formula for the B field from a solenoid (Example 5.9) Rewrite his answer (which is in terms of I) so it is expressed in terms of K (See his Fig 5.34 and 5.35 for help with this). Briefly compare with part 3, do you see any rough connections?

4. Ampere’s Law

Consider a thick SLAB of current.

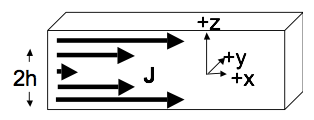
The slab is infinite in (both) $x$ and $y$, but finite in $z$. So we must think about the volume current density $\mathbf{J}$, rather than $\mathbf{K}$. The slab has thickness $2h$ (It runs from $z=-h$ to $z=+h$) Let’s assume that the current is still flowing in the $+x$ direction, and is uniform in the $x$ and $y$ dimensions, but now $\mathbf{J}$ depends on height linearly, i.e. $\mathbf{J} = J_0\,\mathrm{abs}(z)\,\hat{x}$, inside the slab (but is 0 above or below the slab), where $\mathrm{abs}(z)$ is the absolute value of $z$.

1. Find the B field (magnitude and direction) everywhere in space (above, below, and also, most interestingly, inside the slab!)

5. Quick Ampere’s Law

Suppose $\mathbf{B}$ in a region of space centered on the origin has cylindrical symmetry and is given by $\mathbf{B} = B_0\hat{\phi}$ where $B_0$ is a constant, and $\hat{\phi}$ is the azimuthal direction in cylindrical coordinates.

1. What is the current density in this region of space?
2. Suppose the current density that you found extends out to a radius $R$ and is zero for $r > R$. What is the magnetic field for $r > R$?

6. Ampere and superposition

A clever use of superposition should can make seemingly complicated situations easier to solve.

1. A long (infinite) wire (cylindrical conductor of radius $R$, whose axis coincides with the $z$ axis) carries a uniformly distributed current $I_0$ in the $+z$ direction. A cylindrical hole is drilled out of the conductor, parallel to the $z$ axis, (see figure above for geometry). The center of the hole is at $x = b$, and the radius is $a$. Determine the magnetic field in the hole region.
2. If this is an ordinary wire carrying ordinary household currents, and the drilled hole has dimensions roughly shown to scale in the figure above, make an order of magnitude estimate for the strength of the $B$ field in that region. How does it compare to the earth’s field? You should find that the B field in the hole is uniform - that was just a little surprising to me!

7. The magnetic bottle (EXTRA CREDIT)

On Homework 11, you developed a visualization for the magnetic dipole. Here’s a jupyter notebook that produces that visualization in two-dimesions (download it or view it here). In this problem, you will add a second dipole of the same strength that points in the same direction as the previous one and investigate the motion of a charged particle in that magnetic field.

1. Place one magnetic dipole at $z = 10.0$, and the other at $z=−10.0$. Let both dipole moments point in the positive $z$-direction, with equal magnitude $10^4$. Make a vector plot of the resulting magnetic field, and describe your plot.
2. Make a hypothesis about what the charged particle’s trajectory will be shaped like. Based on your vector plot and your physics knowledge, do you predict that the particle will be successfully confined? Why or why not?
3. Add to program to simulate the motion of an $\alpha$-particle in this magnetic field. Start the $\alpha$-particle at position $\langle −5.0,0.0,0.0 \rangle$, with initial velocity $100.0m/s$ in the $z$-direction. Plot the $\alpha$-particle’s trajectory, and compare with your hypothesis. Also, compare and contrast this result with the $\alpha$-particle’s trajectory in the uniform magnetic field in Homework 11 - Problem 4. If you need help modeling this motion, the solution to Homework 11 Problem 4 is posted on SLACK. You may use what you need from this code.
4. For further insight into the charged particle’s trajectory, make a plot of the particle’s $z$-coordinate vs. time. What does this plot tell you about the particle’s motion? Is the particle successfully confined, or do you think it will eventually escape?