Homework 3 (Due September 20th)

Homework 3 emphasizes alternative methods to direct integration (Coulomb’s Law) for solving the electric field problem including the use of Gauss’ Law and reducing the vector problem to a scalar one by using electric potential. In addition, it introduces the concept of the Dirac delta function as a tool for describing distributions of charge. This homework makes use of what you learned in Secs. 1.5, 2.2, and 2.3 (up to about 2.3.2), but what you know from 2.1 (i.e., superposition of ($\mathbf{E}$) will also be important).

Dropbox file request link for Homework 3

1. Numerical Superposition - Electric field of a line charge

As we discussed in class, you can break up a disutrubiton of charge into chunks - each a point charge - and add up the contirubtions to the electric field of each chunk. This process forms the basis of numerical superposition, which you began to explore in the last homework - problem 3. In this problem, you will extend that work to a line of charge. You will solve this problem using a Jupyter notebook. You can download it here (or view it here).

Using numerical superposition, adding up the contributions to the electric field due to each chunk, you will solve the following problems.

1. We want to compute and represent the electric field of the charge at a distance of $0.1 m$ from the line charge along the $y$-axis. Do this.
2. The analytical formula for the electric field of the rod at that location is: $E_{rod} = \dfrac{1}{4\pi\varepsilon_0}\dfrac{Q}{y\sqrt{L^2/4+y^2}}$. Compare the value of the electric field at that location for different values of ‘Nchunks’, say for 10, 20, 50, and 100 chunks. How close do you get with 100 chunks? How many chunks do you need to get within 1% of the analytical solution?
3. Using what you have built to find the electric field at this location, find the electric field at a variety of points around the the line charge and represent them with arrows. You can choose the locations, but be systematic.

2. Comparing Coulomb’s Law to Gauss’ Law

Now that we have, in principle, fully described how to solve any electrostatics problem (i.e., by adding up the contribution of each chunk of charge), we turn to building our theoretical toolbox by learning alternative methods that make the solving of certain kinds of problems more tractable. The first of these alternatives is Gauss’ Law. It is important to know when and how to apply Gauss’ Law - in the problem below, you are asked to compare Gauss’ Law with Coulomb’s Law.

Consider the following questions in finding the electric field everywhere for a conducting sphere, a uniformly charged sphere, and a sphere with charge distribution varying as $r^n$, all with radius $r_0$ and total charge $Q$:

1. What are the advantages and disadvantages of using Gauss’ Law to find the electric field instead of using Coulomb’s Law (Griffiths Eq 2.8)? What role does symmetry play?
2. Answer the same questions for three cubes with the same properties (i.e., charge distributions that vary radially as $r^n$).
3. What do your answers to parts 1 and 2 tell you about using Gauss’ Law versus using Coulomb’s Law (direct integration) to solve for the electric field?

3. Spherical charge distributions are special & GRE Prep

As you might have picked up by now, spherically symmetric charge distributions are very special. We have a number of theoretical tools we can bring to bear on them and the results we produce are often quite simple in a mathematical sense. In this problem, you will explore these distributions a bit more and connect the mathematics (i.e., the integrals you must do) to the geometry of the problem (i.e., where the charge lives) to gain intuition about these spherically symmetric distributions of charge.

For parts 1 and 2, consider a sphere of radius $R$, centered one the origin, with a radially symmetric charge distribution $\rho(r)$.

1. What $\rho(r)$ is required for the electric field in the sphere to have the power law form $E(r) = cr^n$, where $c$ and $n$ are constants? The case of n=-2 is special. How so? Some values of $n$ are unphysical because these would lead to an infinite amount of charge in the sphere.. Which values of $n$ are allowed?
2. What kind of charge distribution is required for the radial E-field inside the sphere to be of constant magnitude; that is, what $\rho(r)$ produces $E(r) = $ constant (inside only)? Is this distribution physical realizable? Why or why not?
3. For each of these allowable charge distributions, what does the electric field look like outside the sphere ($r>R$)?
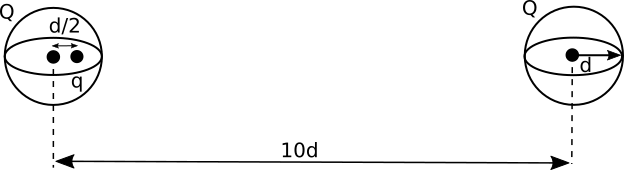
4. GRE Prep: Two spherical, nonconducting, and very thin shells of uniformly distributed positive charge $Q$ and radius $d$ are located a distance 10$d$ apart. A positive point charge $q$ is placed inside on of the shells at a distance $d/2$ from the center, on the line connecting the centers of the two shells, as shown in the figure. What is the net force on the charge $q$?

4. Cube with a hole

What happens when you have problems were the symmetries are mixed? How do you tackle a problem with two different geometries? In this problem, you will explore how to deal with situations where they are two “competing” geometries for the problem. Sometimes you will need to bring two (or more!) aspects of your theoretical toolbox to bear on a problem.

Consider a cube (edge length $a$) with a uniform charge distributed throughout its volume ($\rho$). We carve a spherical cavity out of it of radius $d$, such that the cavity is centered at the center of the cube.

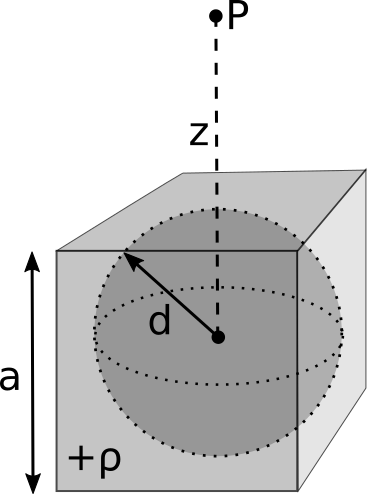
1. Does Gauss’ Law hold for this problem? Can Gauss’ Law be used on this problem? If so, what surface do you use? If not, why?
2. Let the center of the cube (and thus the center of the cavity) be located at the origin $\langle 0,0,0 \rangle$. Explain how you would determine the electric field at point $P$ a distance $z$ from the center of the cube.

5. Describing charge distributions with delta functions

The Dirac delta function is an important theoretical tool for describing distributions of a variety of physical quantities (e.g., mass, charge) where a point object (or system of point objects) is the model we intend to use. In addition, it can be used to describe distributions where these quantities exist in highly constrained spaces (e.g., on a plane or spherical shell). In this class, we will use the Dirac delta function to describe how a charges are distributed. In this problem, you will get familiar with the Dirac delta function for a set point charges on a line.

The linear charge density for a series of charges on the $x$-axis is given by:

\[\lambda(x) = \sum_{n=0}^{10} q_0 n^2\delta\left(x-\dfrac{n}{10}\right)\]

1. Write a sentence or two describing the units of each term in the equation. (Don’t forget the delta function!)
2. What is the total charge on $x$-axis?

6. A rod with a hole drilled in it

Gauss’ Law can be useful in situations where you want to determine the electric field in conceptually different physical spaces. In this problem, you will explore this using the example of a uniformly charged rod with a hole drilled through it.

Consider a rod of length $L$ and radius $b$ that has a hole drilled down the center of it (along it’s length-wise axis) with a radius of $a$. The rod is very long compared to it’s radius, so that Gauss’ Law can be used to find the approximate electric field near the middle of the rod (far from the ends). The rod has a uniform charge distribution $\rho$. You will determine the electric field “everywhere” - meaning everywhere near the middle of the rod.

1. Find the electric field inside the hole ($r<a$).
2. Find the electric field outside the rod ($r>b$).
3. Find the electric field between the hole and outer surface of the rod ($a<r<b$).
4. Why did you need to solve Gauss’ Law 3 times in this case to find the electric field “everywhere”?
5. Compare the value of the electric field right at the material boundaries ($r=a$ and $r=b$), do the values match? As we will find this matching has important implications for bound charge on material surfaces.