Solution Homework 7#
Spring 2025
import numpy as np
from math import *
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
plt.style.use('seaborn-v0_8-colorblind')
Exercise 1 (10pt) Where does the energy go?#
The damped harmonic oscillator is described by the equation of motion is:
where \(m\) is the mass, \(b\) is the damping coefficient, and \(k\) is the spring constant.
The damping term (\(F_{damp} = - b\dot{x}\)) models the dissipative forces acting on the oscillator. The total energy for the oscillator is given by the sum of the kinetic and potential energies,
1a. What is the energy per unit time dissipated by the damping force?
Solution
The energy dissipated per unit time is related to the power of the damping force. The definition of power, which is an instantaneous quantity, is given by the dot product of the force and velocity.
Note that the damping force is opposite to the velocity, so the power is negative. The power is given by:
1b. Take the time derivative of the total energy and show that it is equal (in magnitude) to the energy dissipated by the damping force.
Solution
The time derivative of the total energy is given by:
If we look at the equation of motion, we see that \(m\ddot{x}+kx = -b\dot{x}\), so we can write the time derivative of the energy as:
This is the same as the power dissipated by the damping force.
1c. What is the sign relationship between the energy dissipated by the damping force and the time derivative of the total energy?
Solution
The negative sign in both cases indicate that energy is leaving the system. We expect the energy to decrease over time, and the power dissipated by the damping force is the rate at which the energy is leaving the system.
Exercise 2 (10pt), Unpacking the critically damped solution#
The solution for critical damping (\(\beta = \omega_0\)) is given by,
where \(A\) and \(B\) are constants. Notice the second solution \(x_2(t) = Bte^{-\omega_0t}\) has an additional linear term \(t\). We glossed over this solution in class, but it is important to understand why this term is present because it tells us about solving differential equations with pathologically difficult-to-see solutions.
Start with the under damped solutions,
where we have used the notation \(\omega_1 = \sqrt{\omega_0^2 - \beta^2}\).
2a. Show that you can recover the first solution \(x_1(t)\) by taking the limit of \(\beta \rightarrow \omega_0\) of \(y_1(t)\).
Solution
In the limit that \(\beta \rightarrow \omega_0\), we have \(\omega_1 \rightarrow 0\). This means that the \(\cos(\omega_1 t)\) term in \(y_1(t)\) goes to 1. We are left with \(e^{-\beta t}\cos(\omega_1 t) \rightarrow e^{-\omega_0 t}\). This is the first solution \(x_1(t)\).
2b. Show that you cannot recover the second solution \(x_2(t)\) by taking the limit of \(\beta \rightarrow \omega_0\) of \(y_2(t)\) directly. What do you get?
Solution
In this case, the same limit that \(\omega_1 \rightarrow 0\) means that \(y_2(t) = e^{-\beta t}\sin(\omega_1 t) \rightarrow 0\). This is because the sine function tends to zero. This is not the second solution \(x_2(t)\), but rather the trivial solution \(x_2(t) = 0\). This is not the correct limit to take to recover the second solution.
2c. If \(\beta \neq \omega_0\), you can divide \(y_2(t)\) by \(\omega_1\). Now show that in the limit \(\beta \rightarrow \omega_0\) of \(y_2(t)/\omega_1\), we recover the form of \(x_2(t)\).
Solution
If however, we are careful and divide \(y_2(t)\) by \(\omega_1\), we have:
We can take the limit of this expression as \(\beta \rightarrow \omega_0\), or \(\omega_1 \rightarrow 0\). The core of the expression is:
which we can expand the sine function as a Taylor series:
The limit of the expression is then:
Thus, the limit of \(y_2(t)/\omega_1\) as \(\beta \rightarrow \omega_0\) is:
This gives the form of the second solution \(x_2(t) = Bte^{-\beta t}\).
Exercise 3 (20pt), Exploring the damped harmonic oscillator#
You can choose to solve this exercise using analytical, or graphical methods. Should you decide to use numerical methods, you should make sure to use a method that conserves energy. However, this exercise does not need to be solved numerically as closed form solutions exist.
The solution to the simple harmonic oscillator is given by,
where \(A_{sho}\) and \(B_{sho}\) are determined by the initial conditions. The solution to the underdamped harmonic oscillator is given by,
where \(A\) and \(B\) are also determined by the initial conditions.
Scenario 1#
An undamped oscillator has a period \(T_0 = 1.000\mathrm{s}\), but then the damping is turned on. We observe the period increases by 0.001 seconds.
3a (3pt). What is the damping coefficient \(\beta\)?
Solution
The new period of the damped oscillator is \(T_1 = 1.001\mathrm{s}\). The period of the damped oscillator is given by \(T_1 = 2\pi/\omega_1\). We can solve for the angular frequency \(\omega_1\) and then the damping coefficient \(\beta\).
The relationship between the angular frequency and the damping coefficient is \(\omega_1 = \sqrt{\omega_0^2 - \beta^2}\). We can solve for the damping coefficient,
3b (3pt). By how much does the amplitude of the oscillation decrease after 10 periods?
Solution
The new period is \(T_1=1.001\mathrm{s}\), so the total time for ten periods is \(10T_1 = 10.01\mathrm{s}\). The amplitude of the damped oscillator is given by \(A = A_{sho}e^{-\beta t}\). After ten periods, the fraction it has decayed is
So the amplitude has decreased by 94%.
3c (3pt). What would be able to notice more easily, the change in period or the change in amplitude?
Solution
Definitely the change in amplitude. The change in period is only 0.1% of the original period, which is very difficult to notice. The amplitude, on the other hand, has decreased by 94%, which is very noticeable.
Scenario 2#
An undamped oscillator has a period \(T_0 = 1.000\mathrm{s}\). With weak damping, the amplitude drops by 50% in one period \(T_1\). Recall the period of the damped oscillator is given by \(T_1 = 2\pi/\omega_1\).
3d (3pt). What is the damping coefficient \(\beta\)?
Solution
If we assume weak damping, and we notice the period will not change much, but the amplitude will in one period. Let’s estimate \(T_1 \approx T_0 = 1.000\mathrm{s}\). The amplitude of the damped oscillator is given by \(A = A_{sho}e^{-\beta T_1}\). We know that the amplitude has decreased by 50% in one period, so we can write,
So that the damping coefficient is,
3e (3pt). What is the period of the damped oscillator?
Solution
Here we use that the new frequency is \(\omega_1 = \sqrt{\omega_0^2 - \beta^2}\). The undamped frequency is \(\omega_0 = 2*\pi/T_0\), so that we can compute:
And thus the new period is,
3f (3pt). By how much does the amplitude of the oscillation decrease after 10 periods?
Solution
With \(\beta = 0.693\mathrm{s}^{-1}\), the amplitude of the damped oscillator is given by \(A = A_{sho}e^{-\beta t}\). After ten periods, the fraction it has decayed is,
So the amplitude has decreased by 99.9%.
3g (2pt). What would be able to notice more easily, the change in period or the change in amplitude?
Solution
Definitely the amplitude. The period has changed by 0.6%, which is very difficult to notice. The amplitude, on the other hand, has decreased by 99.9%, which is very noticeable.
Exercise 4 (40pt), The Damped Driven Oscillator#
The damped driven oscillator is described by the equation of motion,
where \(F_0\) is the amplitude of the driving force and \(\omega\) is the frequency of the driving force. We reduced this equation by dividing by \(m\) to get the equation of motion in terms of the damping coefficient \(\beta = b/2m\) and the natural frequency \(\omega_0 = \sqrt{k/m}\). In the equation below, \(f(t) = F_0/m\).
We solve this equation for sinusoidal driving forces, \(f(t) = f_0\cos(\omega t)\) and demonstrated the resonance effect. In this exercise, we will numerically solve the equation of motion. This will allow us to explore the behavior of the damped driven oscillator for different periodic driving forces, not just sinusoidal ones.
Below we have written a numerical solver for the damped undriven oscillator; it’s similar to the prior codes we’ve used. Your task is to modify the code to include a driving force. We have used the second order Runge-Kutta method to solve the equation of motion. You can use the code as a starting point for the damped driven oscillator.
4a (10pt). Modify the code below to include a driving force \(f(t) = f_0\cos(\omega t)\).
To start, choose \(f_0\)=1, \(\omega_0\)=10 and \(\beta\)=0.1.
Check that your code produces a steady state solution for the driven harmonic oscillator. Roughly, what is the steady state amplitude, \(A(t \rightarrow \infty)\), of the driven oscillator?
def driver(t, F0=1.0, omega=10, phase=0.0):
"""
Function defining the driving force.
Can be modified to explore different driving mechanisms.
"""
return F0 * sin(omega * t - phase)
def ddho(y, t, omega_0, beta, F0=1.0, omega=10, phase=0.0):
"""
Function to compute derivatives based on the damped driven oscillator model.
Notice the driving force is included but zero.
"""
x, v = y
dxdt = v
dvdt = -2 * beta * v - omega_0**2 * x + driver(t, F0, omega, phase)
return np.array([dxdt, dvdt])
def rk2_step(y, t, dt, omega_0, beta, F0=1.0, omega=10, phase=0.0):
"""
Performs a single step of the Runge-Kutta 2nd order (midpoint) method.
Parameters:
- y: current state [position, velocity].
- t: current time.
- dt: time step size.
- omega_0: natural frequency of the oscillator.
- beta: damping coefficient.
- F0: amplitude of the driving force.
- omega: frequency of the driving force.
- phase: phase of the driving force.
Returns:
- y_next: state at time step dt [position, velocity].
"""
k1 = ddho(y, t, omega_0, beta, F0, omega, phase)
k2 = ddho(y + 0.5 * k1 * dt, t + 0.5 * dt, omega_0, beta, F0, omega, phase)
y_next = y + k2 * dt
return y_next
# Simulation parameters
T = 100.0 # total time
dt = 0.01 # time step
omega_0 = 9 # natural frequency
beta = 0.1 # damping coefficient
steps = int(T / dt)
t = np.linspace(0, T, steps)
y = np.zeros((steps, 2)) # Array to hold position and velocity
## Initial conditions
y[0] = [0.25, 0.0] # x=1, v=0
for i in range(steps - 1):
y[i + 1] = rk2_step(y[i], t[i], dt, omega_0, beta)
oscillator = pd.DataFrame(y, columns=["Position", "Velocity"])
oscillator["Time"] = t
# Plotting the results
plt.figure(figsize=(10, 8))
plt.plot(oscillator["Time"], oscillator["Position"], label="Position")
plt.axhline(0, color="black", linewidth=1)
plt.xlabel("Time")
plt.ylabel("Position")
plt.grid(True)
## print the max value of the position near the end of the simulation for the last 10% of the time
maxNearEnd = oscillator["Position"].iloc[-int(steps/10):].max()
plt.plot(oscillator["Time"], maxNearEnd * np.ones(steps), label="Max value near end: {:.2f}".format(maxNearEnd), linestyle="--", color="black")
plt.legend()
<matplotlib.legend.Legend at 0xffff880fa960>
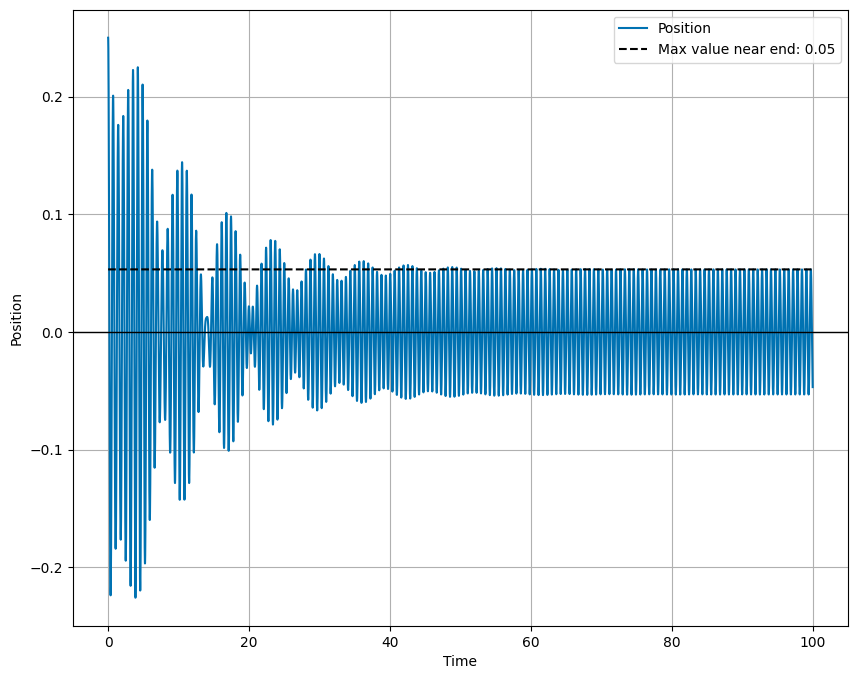
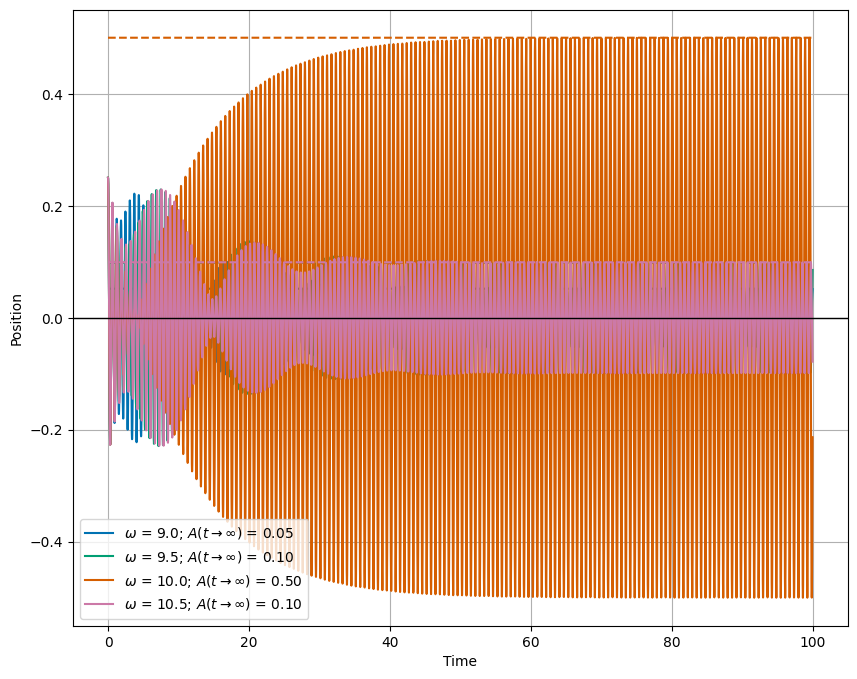
4b (10pt). For different choices of the driving frequency \(\omega\), observe the behavior of the driven oscillator. Describe the behavior of the driven oscillator for \(\omega \ll \omega_0\), \(\omega \approx \omega_0\), and \(\omega \gg \omega_0\).
# Simulation parameters
T = 100.0 # total time
dt = 0.01 # time step
omega_0 = 10 # natural frequency
beta = 0.1 # damping coefficient
steps = int(T / dt)
t = np.linspace(0, T, steps)
y = np.zeros((steps, 2)) # Array to hold position and velocity
## Initial conditions
y[0] = [0.25, 0.0] # x=1, v=0
# Different driving frequencies
omegas = np.arange(9.0, 11.0, 0.5)
plt.figure(figsize=(10, 8))
for omega in omegas:
def driver(t, F0=1.0, omega=omega, phase=0.0):
return F0 * sin(omega * t - phase)
y = np.zeros((steps, 2)) # Reset the array to hold position and velocity for each omega
y[0] = [0.25, 0.0] # Reset initial conditions
for i in range(steps - 1):
y[i + 1] = rk2_step(y[i], t[i], dt, omega_0, beta, F0=1.0, omega=omega, phase=0.0)
oscillator = pd.DataFrame(y, columns=["Position", "Velocity"])
oscillator["Time"] = t
linecolor = "C" + str(np.where(omegas == omega)[0][0])
maxNearEnd = oscillator["Position"].iloc[-int(steps/10):].max()
plt.plot(oscillator["Time"], oscillator["Position"], label=r"$\omega$ = {:.1f}".format(omega)+ r"; $A(t\rightarrow\infty)$ = {:.2f}".format(maxNearEnd), color=linecolor)
plt.plot(oscillator["Time"], maxNearEnd * np.ones(steps), label="", linestyle="--", color=linecolor)
plt.axhline(0, color="black", linewidth=1)
plt.xlabel("Time")
plt.ylabel("Position")
plt.grid(True)
plt.legend()
<matplotlib.legend.Legend at 0xffff61f71b50>
# Simulation parameters
T = 100.0 # total time
dt = 0.01 # time step
omega_0 = 10 # natural frequency
beta = 0.1 # damping coefficient
steps = int(T / dt)
t = np.linspace(0, T, steps)
y = np.zeros((steps, 2)) # Array to hold position and velocity
## Initial conditions
y[0] = [0.25, 0.0] # x=1, v=0
# Different driving frequencies
omegas = np.arange(10.0,10.5,0.1)
plt.figure(figsize=(10, 8))
for omega in omegas:
def driver(t, F0=1.0, omega=omega, phase=0.0):
return F0 * sin(omega * t - phase)
y = np.zeros((steps, 2)) # Reset the array to hold position and velocity for each omega
y[0] = [0.25, 0.0] # Reset initial conditions
for i in range(steps - 1):
y[i + 1] = rk2_step(y[i], t[i], dt, omega_0, beta, F0=1.0, omega=omega, phase=0.0)
oscillator = pd.DataFrame(y, columns=["Position", "Velocity"])
oscillator["Time"] = t
linecolor = "C" + str(np.where(omegas == omega)[0][0])
maxNearEnd = oscillator["Position"].iloc[-int(steps/10):].max()
plt.plot(oscillator["Time"], oscillator["Position"], label=r"$\omega$ = {:.1f}".format(omega)+ r"; $A(t\rightarrow\infty)$ = {:.2f}".format(maxNearEnd), color=linecolor)
plt.plot(oscillator["Time"], maxNearEnd * np.ones(steps), label="", linestyle="--", color=linecolor)
plt.axhline(0, color="black", linewidth=1)
plt.xlabel("Time")
plt.ylabel("Position")
plt.grid(True)
plt.legend()
<matplotlib.legend.Legend at 0xffff61f72150>
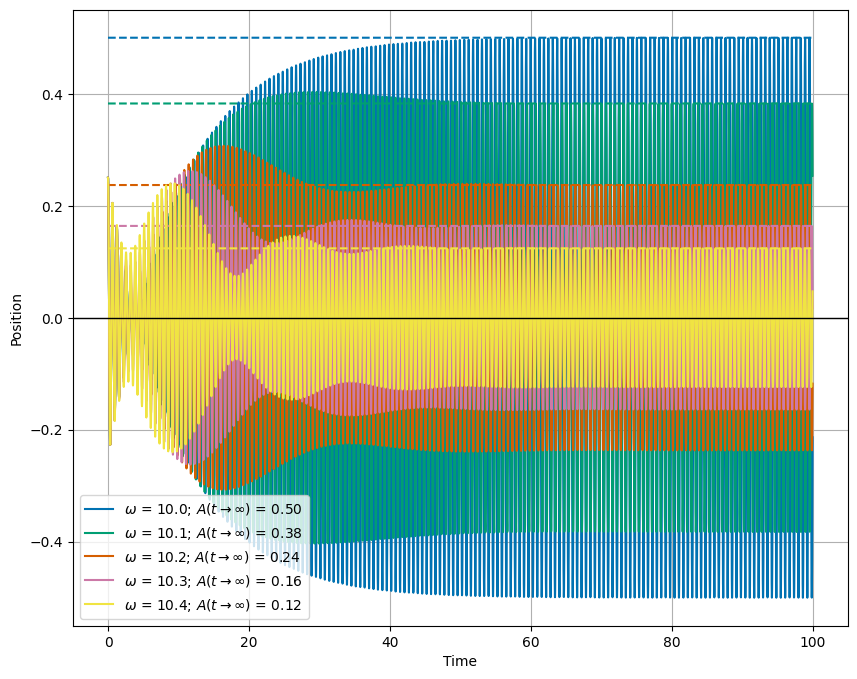
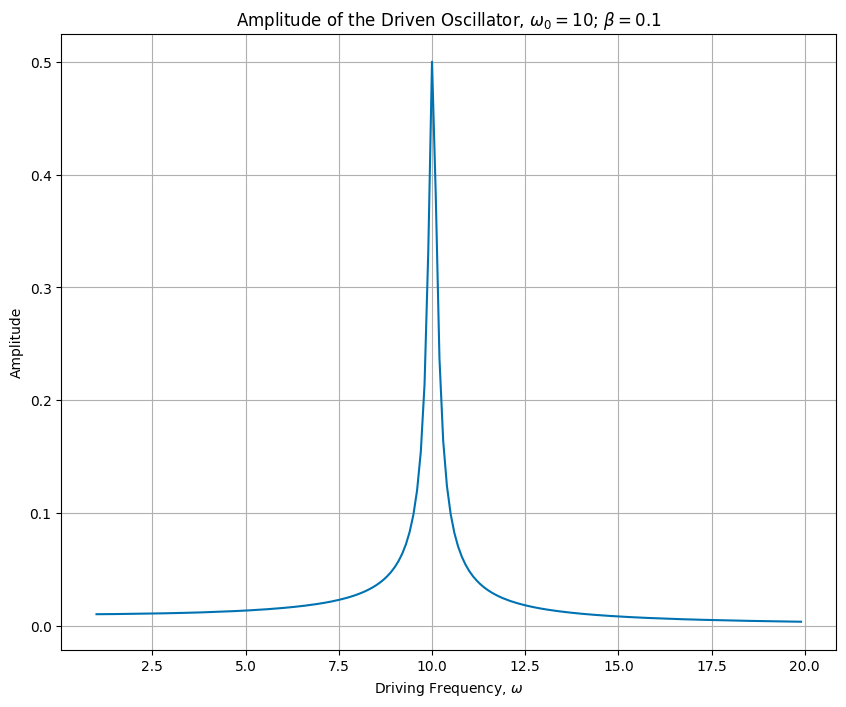
4c (20 pt). Sweep the driving frequency \(\omega\) at a fixed amplitude and store the amplitude of the steady-state solution. Plot the amplitude of the steady-state solution as a function of the driving frequency \(\omega\). Describe the behavior of the amplitude as a function of the driving frequency.
# Simulation parameters
T = 100.0 # total time
dt = 0.01 # time step
omega_0 = 10 # natural frequency
beta = 0.1 # damping coefficient
steps = int(T / dt)
t = np.linspace(0, T, steps)
y = np.zeros((steps, 2)) # Array to hold position and velocity
## Initial conditions
y[0] = [0.25, 0.0] # x=1, v=0
# Different driving frequencies
omegas = np.arange(1.0, 20.0, 0.1)
amplitudes = np.zeros(len(omegas))
dataArray = pd.DataFrame(columns=["Frequency", "Amplitude"])
for omega in omegas:
def driver(t, F0=1.0, omega=omega, phase=0.0):
return F0 * sin(omega * t - phase)
y = np.zeros((steps, 2)) # Reset the array to hold position and velocity for each omega
y[0] = [0.25, 0.0] # Reset initial conditions
for i in range(steps - 1):
y[i + 1] = rk2_step(y[i], t[i], dt, omega_0, beta, F0=1.0, omega=omega, phase=0.0)
oscillator = pd.DataFrame(y, columns=["Position", "Velocity"])
oscillator["Time"] = t
maxNearEnd = oscillator["Position"].iloc[-int(steps/10):].max()
new_row = pd.DataFrame({"Frequency": [omega], "Amplitude": [maxNearEnd]})
dataArray = pd.concat([dataArray, new_row], ignore_index=True)
/tmp/ipykernel_4565/2430410779.py:36: FutureWarning: The behavior of DataFrame concatenation with empty or all-NA entries is deprecated. In a future version, this will no longer exclude empty or all-NA columns when determining the result dtypes. To retain the old behavior, exclude the relevant entries before the concat operation.
dataArray = pd.concat([dataArray, new_row], ignore_index=True)
plt.figure(figsize=(10, 8))
plt.plot(dataArray["Frequency"], dataArray["Amplitude"])
plt.xlabel(r"Driving Frequency, $\omega$")
plt.ylabel("Amplitude")
plt.title(r"Amplitude of the Driven Oscillator, $\omega_0 ="+str(omega_0)+r"$; $\beta ="+str(beta)+r"$")
plt.grid()
plt.show()
Exercise 5 (20pt), Project Check-in 1#
This is the first of three check-ins for your final project. Last week, you submitted a project proposal with milestones. This week, you will submit a progress report. This is common in science and engineering research. Funding agencies require an annual report to ensure the project is on track. While we are not funding you, we want this work to be a similar experience to a research project.
The first annual report is often a minimal progress report. How much can you say? You have only just started!
But, you can say what you have done, what you are planning to do, what you have learned so far, and what changes you have to make. This is the purpose of this exercise.
5a (5 pts). Review your project proposal. What have you been able to accomplish so far? What were you unable to do in the time you had? Be honest in your evaluation of your progress. You will not be penalized for not reaching your milestones. What does that mean you need to prioritize in the coming weeks? (at least 250 words)
5b (5 pts). What problems did you encounter in doing you research? What questions came up and how did you resolve them? Are there any unresolved questions? (at least 250 words)
5c (5 pts). Provide an artifact from your project. This could be a plot, a code snippet, a data set, or a figure. Explain what this artifact is and how it fits into your project. (at least 100-200 words)
5d (5 pts). Update your project timeline and milestones. How will you adjust your timeline to account for the work you have done and the work you have left to do? (at least 100-200 words)
Extra Credit - Integrating Classwork With Research#
This opportunity will allow you to earn up to 5 extra credit points on a Homework per week. These points can push you above 100% or help make up for missed exercises. In order to earn all points you must:
Attend an MSU research talk (recommended research oriented Clubs is provided below)
Summarize the talk using at least 150 words
Turn in the summary along with your Homework.
Approved talks: Talks given by researchers through the following clubs:
Research and Idea Sharing Enterprise (RAISE): Meets Wednesday Nights Society for Physics Students (SPS): Meets Monday Nights
Astronomy Club: Meets Monday Nights
Facility For Rare Isotope Beam (FRIB) Seminars: Occur multiple times a week
