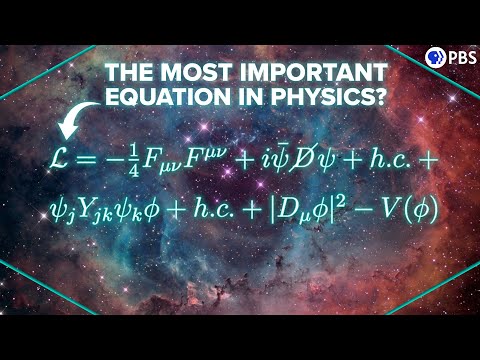Week 13 - Lagrangian Mechanics

The Lagrangian formulation of mechanics allows us to describe the motion of a system in terms of its kinetic and potential energy, rather than its forces. This approach is particularly useful for systems with constraints or when dealing with generalized coordinates. There’s a few general concepts that arise in Lagrangian mechanics that make it a powerful tool for analyzing mechanical systems.

First, the Lagrangian formulation emphasizes the idea of independent coordinates while also providing the flexibility to use any set of coordinates that are convenient for the problem at hand. This is in contrast to Newtonian mechanics, which often relies clearly structured position and velocity vectors.

Because the Lagrangian uses this generalized coordinate system, it is often easier to analyze complex systems with many degrees of freedom. Moreover, when dealing with constraints, the Lagrangian formulation allows us to incorporate these constraints directly into the equations of motion, which reduces the dimensionality of the problem.

In addition, the Lagrangian formulation is particularly useful for systems with symmetries. By applying Noether’s theorem, we can relate symmetries of the system to conserved quantities, which can simplify the analysis of the system’s motion. For example, if a particular system is invariant under time translations (for us no explicit time dependence in \(\mathcal{L}\)), we can conclude that energy is conserved. If a coordinate is cyclic (e.g., no \(x\) dependence in \(\mathcal{L}\)), we can conclude that the corresponding momentum (in this example, \(p_x\)) is conserved.

Lastly, the formalism produces generalized forces that are not necessarily equal to the physical forces acting on the system, but have corresponding generalized momenta. These are always produced in our equations of motion, but they might not be forces or momenta that we can measure directly, or that we can even define as a “force”, some are torques, for example.

Consider an \(N\) dimensional system with \(N\) generalized coordinates \(q_i\) and \(N\) generalized velocities \(\dot{q}_i\). The Lagrangian is defined as the difference between the kinetic energy \(T\) and the potential energy \(V\) of the system:

\[ \mathcal{L} = T(\dot{q}_1, \dot{q}_2, \dots, \dot{q}_N) - V(q_1, q_2, \dots, q_N) \]

The derivative of the Lagrangian with respect to a generalized coordinate \(q_i\) is given by:

\[\dfrac{\partial \mathcal{L}}{\partial q_i} = \dfrac{\partial V}{\partial q_i} = F_{q_i}\]

where \(F_{q_i}\) is the generalized force conjugate to the coordinate \(q_i\).

The derivative of the Lagrangian with respect to a generalized velocity \(\dot{q}_i\) is given by:

\[\dfrac{\partial \mathcal{L}}{\partial \dot{q}_i} = \dfrac{\partial T}{\partial \dot{q}_i} = p_{q_i}\]

where \(p_{q_i}\) is the generalized momentum conjugate to the coordinate \(q_i\).

The Standard Model Lagrangian (17 minute video)

An understanding of physics formulated through Lagrangian Mechanics is a powerful and elegant way to describe the motion of particles and systems. But it can be much more than that. Much of the work of particle physics is done in the context of the Standard Model. The Standard Model is a theory that describes the electromagnetic, weak, and strong nuclear interactions. The Standard Model is a quantum field theory, which is formulated through a Lagrangian.

The video below provides an introduction to this equation and the Standard Model.