Solution Homework 6

Spring 2025

import numpy as np
from math import *
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
plt.style.use('seaborn-v0_8-colorblind')

Exercise 1 (10pt) Morse Potential as an SHO

If the potential has a local minimum, we can often find SHO approximation for that potential near the local minimum.

The Morse potential is a convenient model for the potential energy of a diatomic molecule. The potential is a radial one and thus one-dimensional. It is given by,

\[U(r) = A\left[ \left(e^{(R-r)/S}-1\right)^2-1\right]\]

where the distance between the centers of the two atoms is \(r\), and the constants \(A\), \(R\), and \(S\) are all positive. Here \(S<<R\).

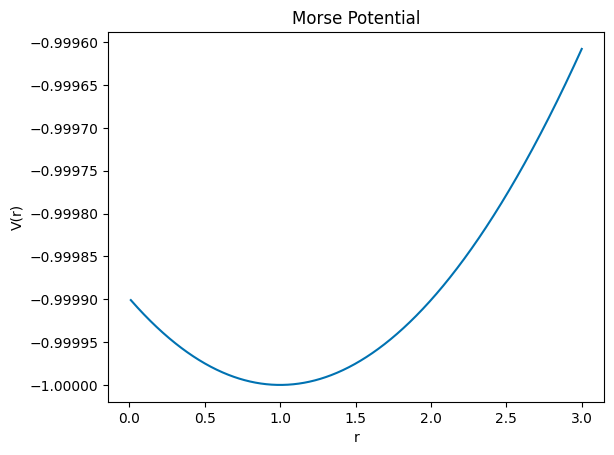
• 1a (2pt) Sketch (or plot) the potential as a function of \(r\).

SOLUTION

We can plot the Morse potential, but we need to choose some values for the constants. Let’s choose \(A=1\), \(R=1\), and \(S=0.01\).

def MorsePotential(r, A=1, R=1, S=0.01):
    
    return A * ((np.exp(-S * (r - R)) - 1)**2 - 1)

r = np.linspace(0.01, 3, 1000)
plt.plot(r, MorsePotential(r))
plt.xlabel('r')
plt.ylabel('V(r)')
plt.title('Morse Potential')

Text(0.5, 1.0, 'Morse Potential')

• 1b (3pt) Find the equilibrium position of the potential, i.e. the position where the potential is at a minimum. We will call this \(r_e\).

SOLUTION

The equilibrium position is found by taking the derivative of the potential and setting it equal to zero. So we have,

\[\frac{dU}{dr} = 0 = -2A\left(e^{(R-r)/S}-1\right)\left(e^{(R-r)/S}\right)\left(-\frac{1}{S}\right).\]

We can solve for \(r\) to find the equilibrium position.

\[0 = 2A\left(e^{(R-r)/S}-1\right)\left(e^{(R-r)/S}\right)\left(-\frac{1}{S}\right).\]

If we are looking for a finite solution, we focus on the first term in the product.

\[0 = \left(e^{(R-r)/S}-1\right),\]

\[1 = e^{(R-r)/S},\]

\[\ln(1) = \frac{R-r}{S},\]

\[0 = \frac{R-r}{S},\]

\[r_e = R.\]

• 1c (3pt) Rewrite the potential in terms of the displacement from equilibrium, \(r = r_e + x\). Expand the potential to second order in \(x\).

SOLUTION

We can expand the potential to second order in \(x\) by using the Taylor expansion. First we plugin \(r = r_e + x = R+x\) into the potential.

\[U(r_e+x) = A\left[ \left(e^{(R-(r_e+x))/S}-1\right)^2-1\right],\]

\[U(R+x) = A\left[ \left(e^{(R-R-x)/S}-1\right)^2-1\right],\]

\[U(x) = A\left[ \left(e^{-x/S}-1\right)^2-1\right].\]

So now we expand the potential to second order in \(x\).

\[U(x) \approx A\left[ \left(1-\frac{x}{S}+\frac{x^2}{S^2}-1\right)^2-1\right],\]

\[U(x) \approx A\left[ \left(-\frac{x}{S} + \frac{x^2}{S^2}\right)^2-1\right],\]

\[U(x) \approx -A + A\left[ \frac{x^2}{S^2}\right].\]

• 1d (2pt) Find the effective spring constant, \(k\), for the potential near the minimum. What is the frequency of small oscillations about the minimum?

SOLUTION

We can use the simple harmonic potential to find the effective spring constant. For the SHO,

\[U(x) = \frac{1}{2}kx^2 + U_0,\]

where \(U_0\) is the potential at the minimum. We can compare this to the expansion of the approximate Morse potential to find the effective spring constant.

\[U(x) \approx -A + A\left[ \frac{x^2}{S^2}\right].\]

Such that,

\[U_0 = -A \quad \text{and} \quad k = \frac{2A}{S^2}.\]

For a particle of mass \(m\), the frequency of small oscillations about the minimum is,

\[\omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{2A}{mS^2}}.\]

Exercise 2 (10pt), Time Averaging and the SHO

Time Averaging is a common tool to use with periodic systems. It also us to discuss what happens to different properties of the system over one period.

An SHO has a period \(\tau\). We can find the time average of a variable \(f(t)\) over one period, \(\langle f \rangle\), by averaging over the period,

\[\langle f \rangle = \frac{1}{\tau}\int_0^\tau f(t)dt\]

• 2a (2pt) Show that the time average of the position of the SHO is zero.

SOLUTION

Let’s the take the general case of the SHO. It’s position is given by,

\[x(t) = A\cos(\omega t - \delta),\]

where \(A\) is the amplitude, \(\omega\) is the angular frequency, and \(\delta\) is the phase. The time average of the position can be constructed from the integral prescription above,

\[\langle x \rangle = \frac{1}{\tau}\int_0^\tau A\cos(\omega t - \delta)dt.\]

We convert the angular frequency to the period, \(\omega = \frac{2\pi}{\tau}\), and the integral becomes,

\[\langle x \rangle = \frac{1}{\tau}\int_0^\tau A\cos\left(\frac{2\pi t}{\tau} - \delta\right)dt.\]

We now integrate the cosine function over one period and evaluate it,

\[\langle x \rangle = \frac{A}{\tau} \frac{\tau}{2\pi} \left[ \sin \left( \frac{2\pi t}{\tau} - \delta \right) \right]_0^\tau,\]

\[\langle x \rangle = \frac{A}{2\pi} \left[ \sin \left( 2\pi - \delta \right) - \sin \left( -\delta \right) \right].\]

So we are computing the difference of the sine function at two different points, but precisely one period apart (\(2\pi\)). The value of the function is the same at both points. So the time average of the position is zero,

\[\langle x \rangle = \frac{A}{2\pi} \left[ \sin \left( -\delta \right) - \sin \left( -\delta \right) \right],\]

\[\langle x \rangle = 0.\]

• 2b (2pt) Show that the time average of the velocity of the SHO is zero.

SOLUTION

Our solution from above is fairly general. The velocity of this SHO is,

\[v(t) = -A\omega\sin(\omega t - \delta).\]

We see that we will get an integral with the same form as before,

\[\langle v \rangle = \frac{1}{\tau}\int_0^\tau -A\omega\sin(\omega t - \delta)dt,\]

\[\langle v \rangle = \frac{-A\omega}{\tau}\int_0^\tau \sin\left(\frac{2\pi t}{\tau} - \delta\right)dt.\]

This integral evaluates no differently from the prior one. We take the difference of the integrated periodic function exactly one period apart. This will result in a zero time average as well.

\[\langle v \rangle = 0.\]

• 2c (6pt) Show that the time average of the kinetic energy of the SHO is equal to the time average of the potential energy (and importantly, non-zero). If the total energy is \(E\), these time averages are equal to \(E/2\). You might need to show that the very useful trigonometric identity,

\[\langle \sin^2(\omega t-\delta)\rangle = \langle \cos^2(\omega t-\delta)\rangle = \frac{1}{2}\]

SOLUTION

The energies of the SHO are,

\[K(t) = \frac{1}{2}m\left(-A\omega\sin(\omega t - \delta)\right)^2,\]

\[U(t) = \frac{1}{2}k\left(A\cos(\omega t - \delta)\right)^2.\]

So we know that we will have to compute the time average of the square of the sine and cosine functions. So let’s just do that first,

\[\langle \sin^2(\omega t-\delta)\rangle = \frac{1}{\tau}\int_0^\tau \sin^2\left(\frac{2\pi t}{\tau} - \delta\right)dt.\]

We can use the trigonometric identity \(\sin^2(x) = \frac{1}{2}(1 - \cos(2x))\) to simplify the integral,

\[\langle \sin^2(\omega t-\delta)\rangle = \frac{1}{\tau}\int_0^\tau \frac{1}{2}\left(1 - \cos\left(\frac{4\pi t}{\tau} - 2\delta\right)\right)dt.\]

We separate the integral into two parts,

\[\langle \sin^2(\omega t-\delta)\rangle = \frac{1}{2} - \frac{1}{2\tau}\int_0^\tau \cos\left(\frac{4\pi t}{\tau} - 2\delta\right)dt.\]

As before, we notice the integral of the cosine function over one period evaluates to zero. So are left with,

\[\langle \sin^2(\omega t-\delta)\rangle = \frac{1}{2}.\]

We can make a similar argument for the cosine function by using the trigonometric identity \(\cos^2(x) = \frac{1}{2}(1 + \cos(2x))\). This would also give us,

\[\langle \cos^2(\omega t-\delta)\rangle = \frac{1}{2}.\]

And thus the time average of the kinetic and potential energies are,

\[\langle K \rangle = \frac{1}{2}m\omega^2A^2\langle \sin^2(\omega t-\delta)\rangle = \frac{1}{4}m\omega^2A^2,\]

\[\langle U \rangle = \frac{1}{2}kA^2\langle \cos^2(\omega t-\delta)\rangle = \frac{1}{4}kA^2.\]

We note that \(k = m\omega^2\), so the time averages are equal,

\[\langle K \rangle + \langle U \rangle = \frac{1}{4}kA^2 + \frac{1}{4}kA^2 = \frac{1}{2}kA^2.\]

For an SHO with amplitude \(A\) (as we constructed), the total energy is \(E = \frac{1}{2}kA^2\), so the time averages are equal to \(E/2\).

Exercise 3 (10pt), Toy Potential

Consider a toy potential of the form,

\[U(r) = U_0\left(\dfrac{r}{R}+\lambda^2\frac{R}{r}\right)\]

where \(U_0\), \(R\), and \(\lambda\) are all positive constants and the domain of the potential is \(0<r<\infty\).

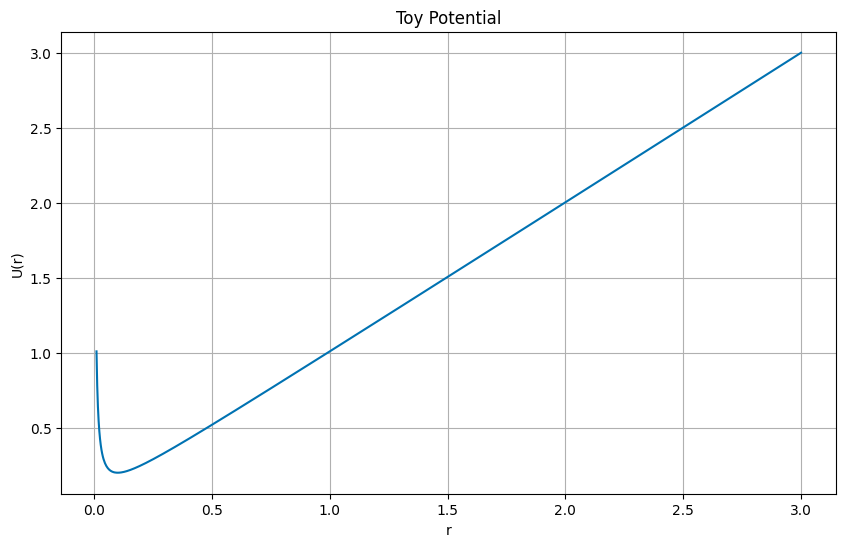
• 3a (2pt) Sketch (or plot) the potential as a function of \(r\).

SOLUTION

We can plot the toy potential, but we need to choose some values for the constants. Let’s choose \(U_0=1\), \(R=1\), and \(\lambda=0.1\). Thus,

\[U(r) = 1\left(\dfrac{r}{1}+0.1^2\frac{1}{r}\right).\]

def ToyPotential(r, U0=1, R=1, lambda_=0.1):
    return U0*(r/R+lambda_**2*R/r)

r = np.linspace(0.01, 3, 1000)

fig = plt.figure(figsize=(10, 6))
plt.plot(r, ToyPotential(r))
plt.xlabel('r')
plt.ylabel('U(r)')
plt.title('Toy Potential')
plt.grid(True)

• 3b (3pt) Find the equilibrium position of the potential, i.e. the position where the potential is at a minimum. We will call this \(r_e\).

SOLUTION

To find the equilibrium position, we take the derivative of the potential and set it equal to zero. So we have,

\[\frac{dU}{dr} = 0 = U_0\left(\dfrac{1}{R}-\lambda^2\frac{1}{r^2}\right).\]

We can solve for \(r\) to find the equilibrium position.

\[0 = \dfrac{1}{R}-\lambda^2\frac{1}{r^2},\]

\[\lambda^2\frac{1}{r^2} = \dfrac{1}{R},\]

\[r^2 = \lambda^2R,\]

\[r_e = \pm\lambda R.\]

We take the positive root, \(r_e = \lambda R\), as the equilibrium position because the potential is symmetric about the origin.

• 3c (5pt) Rewrite the potential in terms of the displacement from equilibrium, \(r = r_e + x\). Expand the potential to second order in \(x\). What is the effective spring constant, \(k\), for the potential near the minimum? What is the frequency of small oscillations about the minimum?

SOLUTION

We can expand the potential to second order in \(x\) by using the Taylor expansion. First we plugin \(r = r_e + x = \lambda R + x\) into the potential.

\[U(r_e+x) = U_0\left(\dfrac{\lambda R + x}{R}+\lambda^2\frac{R}{\lambda R + x}\right).\]

We multiple this out to get,

\[U(r_e+x) = U_0\left(\lambda + \dfrac{x}{R}+\lambda^2\frac{R}{\lambda R + x}\right).\]

We can clean up the last term by taking out an \(\lambda R\) from the denominator and then Taylor expanding the result,

\[U(r_e+x) = U_0\left(\lambda + \dfrac{x}{R}+\frac{\lambda^2R}{\lambda R}\frac{1}{1+\frac{x}{\lambda R}}\right),\]

\[U(r_e+x) = U_0\left(\lambda + \dfrac{x}{R}+\lambda \left(1-\frac{x}{\lambda R}+\frac{x^2}{(\lambda R)^2}-\frac{x^3}{(\lambda R)^3}+\cdots\right)\right).\]

Keeping only the terms up to second order in \(x\),

\[U(x) \approx U_0\left(\lambda + \dfrac{x}{R}+\lambda -\frac{x}{R}+\frac{x^2}{(\lambda R)^2}\right),\]

\[U(x) \approx U_0\left(2\lambda + \frac{x^2}{(\lambda R)^2}\right).\]

Matching to the form of the SHO potential, we find the effective spring constant,

\[k = \frac{2U_0}{\lambda^2 R^2}.\]

For a particle of mass \(m\), the frequency of small oscillations about the minimum is,

\[\omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{2U_0}{m\lambda^2 R^2}}.\]

Exercise 4 (10pt), Defining Periodicity

A common issue with oscillators is determining their periodicity. For the SHO, we can show that the period is \(2\pi/\omega_0\) where \(\omega_0\) is the natural frequency of the SHO. How might we define a periodicity more generally? Let’s start with the damped harmonic oscillator. Consider a weakly damped oscillator (\(\beta < \omega_0\)). The motion of the oscillator is given by,

\[x(t) = A e^{-\beta t}\cos(\omega_1 t - \delta)\]

where \(A\) is the amplitude, \(\beta\) is the damping constant, \(\omega_1 = \sqrt{\omega_0^2 - \beta^2}\) and \(\delta\) is the phase.

The motion decays with time, but we can still define a periodicity, \(\tau_1\), which is the time between peaks in the motion.

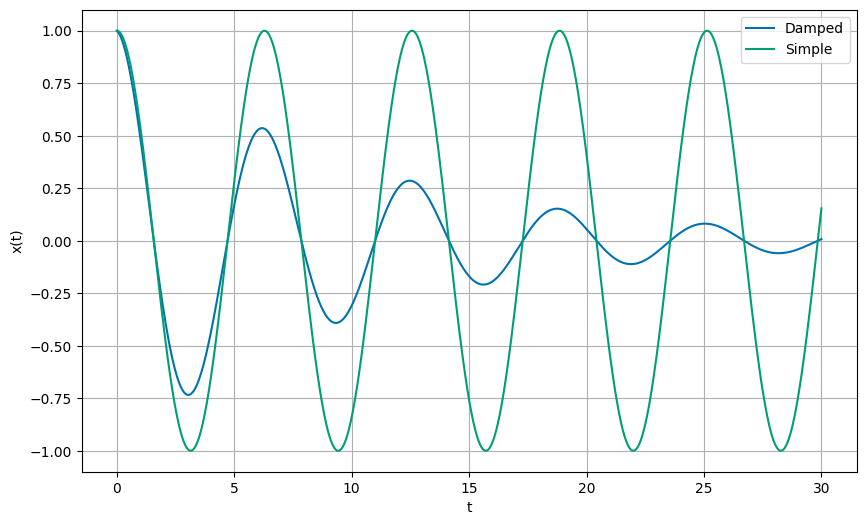
• 4a (4pt) Sketch (or plot) the motion of the oscillator as a function of time. Show that you can find \(\tau_1 = 2\pi/\omega_1\) from looking at successive maxima.

SOLUTION

We can plot the motion of the oscillator, but we need to choose some values for the constants. Let’s choose \(A=1\), \(\beta=0.1\), and \(\omega_0=1\). Thus,

\[x(t) = e^{-0.1 t}\cos(\sqrt{1-0.01} t - \delta).\]

We can plot this function and look for the time between successive maxima. We can then compare this to an SHO with a frequency equal to \(\omega_1\).

It’s easy to see from the graph that each maximum in the damped oscillator occurs at the peak of the SHO with the same frequency. This is the definition of the period of the damped oscillator, \(\tau_1 = 2\pi/\omega_1\).

def DampedOscillator(t, A=1, omega=1, gamma=0.1, delta=0):
    return A * np.exp(-gamma * t) * np.cos(omega * t - delta)

def SHO(t, A=1, omega=1, delta=0):
    return A * np.cos(omega * t - delta)

t = np.linspace(0, 30, 1000)

fig = plt.figure(figsize=(10, 6))
plt.plot(t, DampedOscillator(t))
plt.plot(t, SHO(t))
plt.legend(['Damped', 'Simple'])
plt.grid(True)
plt.xlabel('t')
plt.ylabel('x(t)')

Text(0, 0.5, 'x(t)')

• 4b (3pt) Show that an equivalent definition of \(\tau_1\) is twice the time between zero crossings of the motion.

SOLUTION

Again, from the graph, we can see that the time between zero crossings is half the time between successive maxima. This is simply another definition of the period of the damped oscillator, \(\tau_1 = 2\pi/\omega_1\).

• 4c (3pt) If the damping \(\beta\) is half the natural frequency (\(\omega_0\)), how does the amplitude of the motion decay in one period?

SOLUTION

Using the general solution,

\[x(t) = A e^{-\beta t}\cos(\omega_1 t - \delta),\]

we can see that using the definition of \(\omega_1 = \sqrt{\omega_0^2 - \beta^2}\), we can write the motion as,

\[x(t) = A e^{-\beta t}\cos(\sqrt{\omega_0^2 - \beta^2} t - \delta).\]

With \(\beta = \omega_0/2\), we have,

\[x(t) = A e^{-\omega_0 t/2}\cos\left(\sqrt{\omega_0^2 - \left(\frac{\omega_0}{2}\right)^2} t - \delta\right),\]

\[x(t) = A e^{-\omega_0 t/2}\cos\left(\sqrt{\frac{3\omega_0^2}{4}} t - \delta\right).\]

From this form, we have found the period of this damped oscillator,

\[\tau_1 = \frac{2\pi}{\sqrt{3\omega_0^2/4}} = \frac{4\pi}{\sqrt{3}\omega_0}.\]

And thus the amplitude decays thusly,

\[A e^{-\omega_0 \tau_1/2} = A e^{-2\pi/\sqrt{3}}.\]

Exercise 5 (10pt), Planning your Final Project

The point of this exercise is to get you thinking about what you want to do for a final project and how you will accomplish it. Research and project planning are important skills to develop and it takes time to do so. We are trying to scaffold that development and give you the opportunity to practice these skills. So, you will be responsible for developing a plan for your final project, and the timeline under which you will accomplish it. Our job is to provide feedback and guidance on your plan, and to offer support in the development and construction of your final project.

Remember there is no right or wrong way to do this, it is about developing a plan that works for you.

Your final project is your chance to bring all the tools we have developed to bear on a question that interests you. You have reviewed the information on computational essays before, but here it is again in case it’s useful for this exercise:

1. Wolfram’s What is a Computational Essay?

2. Tor and my short paper: Computational Essays: An Avenue for Scientific Creativity in Physics

3. Wolfram’s Steps to Writing a Computational Essay

4. University of Oslo’s Computational Essay Showroom

For your final project, you may work alone, in pairs, or in groups of up to three people. The expectation for your work will be higher if you have more people in your group; your explorations will need to be more comprehensive and detailed, and your essay will be expected to be longer and more polished if you have more people in your group. You can also develop more interesting ways of presenting your work that demonstrate the creativity and depth of your explorations if you have more people in your group. If you have any questions, just ask.

For this exercise, we want you to get started on planning your final project by sending us a brief proposal with a timeline. To help you, we have provided a schedule where you can see the checkpoints for your project, and when we will have a comprehensive work week. You should take advantage of the work week to make significant progress on your project; especially if there are technical aspects you are unsure about.

Schedule for Final Project

• 28 March - HW 7 will have a request for your 1st project update.

• 11 Apr - Midterm Project 2 will have a request for your 2nd project update.

• 18 Apr - HW 8 will have a request for your 3rd project update.

• Week of 20-24 Apr - Project work week in-class.

• 28 Apr - Final project due.

Your Proposal

Your proposal should be a one to two page, single spaced, document that outlines the following:

1. The question you are interested in exploring. The motivation and interest to you and your group mates should be made clear. That is, motivate the question, why is it interesting?

2. References that provide background for this work. This should include the sites, resources, and references you have consulted to get started.

3. The approach you think you need to take to answer this question. Include the concepts and tools you plan to use to explore the question. That is, what have we developed in class that you will use to explore the question?

4. The timeline for your project. This should include the checkpoints in the schedule above, and any additional milestones you think are important. Consider making a Gantt chart to help you plan your project. This is a useful tool for planning and tracking your progress. It’s almost expected for proposals in science and engineering. Here, We suggest you take advantage of the work week to make significant progress on or to polish your project.

Your writing

You should consider this a formal proposal. It should be well written, clear, and concise. You should also consider the audience for this proposal. You should write this proposal for someone who is not in this class, but does know physics. Think about writing this to another student, a graduate student, or a professor. Someone that has a good understanding of physics, but not necessarily the details of your physics. You need to explain the motivation, the physics background, the approach, and the timeline in a way that is compelling and clear.

Your proposal need not be long, but it should be complete. Here are some additional resources for you to develop a good proposal:

• NIH, How to write a research proposal?

• University of Sheffield, How to write a research proposal

Reference pages do not count towards the length, so if you have a lot of references, that’s fine. But the main text should be one to two pages. This is how it works with most proposals in science and engineering.

Exercise 6 (50 pt), Find your own 1D Oscillator

We have built all the tools to study 1D unforced oscillators. Now you get to pick your own potential and study it. You can pick any 1D potential you like, but it should have a local minimum. Make sure it is not a driven oscillator (i.e., no explicit time dependence in the equations of motion). To earn full credit for this exercise, you must:

• 6a (5pt) Present the potential and describe its origin, why it is interesting, where it comes from, etc. Educate us about it.

• 6b (5pt) Sketch (or plot) the potential as a function of it’s argument (and chosen variables) and find the equilibrium position of the potential, i.e. the position where the potential is at a minimum.

• 6c (10pt) Rewrite the potential in terms of the displacement from equilibrium. Expand the potential to second order to find the effective spring constant, \(k\), for the potential near the minimum. What is the frequency of small oscillations about the minimum?

• 6d (10pt) Construct the equations of motion for the potential and solve them numerically. Choose initial conditions and parameters that give oscillatory motion. Note it doesn’t have to be SHO (In fact, it probably won’t be). Plot the position as a function of time. Make sure we can see the oscillations.

• 6e (10pt) Plot the phase diagram of the trajectory (you don’t have to produce a phase diagram, but just plot the trajectory in phase space). What does the phase diagram tell you about the motion?

• 6f (10pt) Find the period of your motion. Here you might have to make some definitions of what periodicity means for your potential.

Note: this might seem similar to your midterm, but notice we expect you to do some research on the potential in 6a, and we are going into more depth with questions 6e and 6f. This is also a scaffold for your final project in terms of practicing aspects that should appear.

Examples of 1D potentials

1. Simple Pendulum (Nonlinear Small Angle Approximation):

   • Potential: \( V(\theta) = mgh(1 - \cos(\theta)) \), where \(m\) is the mass, \(g\) is the acceleration due to gravity, \(h\) is the length of the pendulum, and \(\theta\) is the angular displacement.

2. Nonlinear Spring (Hardening or Softening):

   • Potential: \( V(x) = \frac{k}{2} x^2 + \frac{\beta}{3} x^3 \), where \(k\) and \(\beta\) are constants. Depending on the sign of \(\beta\), the spring can exhibit hardening (\(\beta > 0\)) or softening (\(\beta < 0\)) nonlinearity.

3. Lennard-Jones Potential Oscillator (for a diatomic molecule model):

   • Potential: \( V(r) = 4\epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6 \right] \), where \(\epsilon\) is the depth of the potential well, \(\sigma\) is the finite distance at which the inter-particle potential is zero, and \(r\) is the distance between particles.

4. Morse Potential (for molecular vibrations):

   • Potential: \( V(x) = D_e \left(1 - e^{-a(x - x_0)}\right)^2 \), where \(D_e\) is the depth of the potential well, \(a\) is a constant related to the width of the well, \(x\) is the displacement from equilibrium, and \(x_0\) is the equilibrium bond length. This potential models the energy of a diatomic molecule as a function of the distance between atoms, showing oscillatory behavior that represents molecular vibrations.

5. Double Well Potential:

   • Potential: \( V(x) = -\frac{\mu}{2} x^2 + \frac{\lambda}{4} x^4 \), where \(\mu\) and \(\lambda\) are positive constants. This system exhibits bistability with two stable equilibria, leading to interesting nonlinear dynamics and potential oscillations between the wells under certain conditions.

Extra Credit - Integrating Classwork With Research

This opportunity will allow you to earn up to 5 extra credit points on a Homework per week. These points can push you above 100% or help make up for missed exercises. In order to earn all points you must:

1. Attend an MSU research talk (recommended research oriented Clubs is provided below)

2. Summarize the talk using at least 150 words

3. Turn in the summary along with your Homework.

Approved talks: Talks given by researchers through the following clubs:

• Research and Idea Sharing Enterprise (RAISE)​: Meets Wednesday Nights Society for Physics Students (SPS)​: Meets Monday Nights

• Astronomy Club​: Meets Monday Nights

• Facility For Rare Isotope Beam (FRIB) Seminars: ​Occur multiple times a week