Homework 6 (Due. Feb 22)
1. Leading and Lagging Current
The phase difference between different measurable aspects of a circuit (e.g., voltage and current) are important in a variety of experimental setups. In this question, you will explore this idea a bit more by doing some of your own research and critiquing two different ways of representing current and voltage measures.
- Start by reading about leading and lagging current. You can read the wikipedia article, but any other reputable site is fine as well. Summarize what leading and lagging current is and how it’s defined.
- Consider a standard RLC circuit with each circuit element in series with the next. The whole circuit is driven with an AC voltage $V=V_0\cos(\omega t)$. Find the real current through the voltage source using the method of phasors ($\widetilde{V} = \widetilde{I}\widetilde{Z}$).
- Can you determine if the phase you found in part 2 is positive or negative? What governs the sign of the phase?
- Assume that $1/(\omega C) > \omega L$. Sketch $Z_{tot}$ in the complex plane. Separately sketch $\widetilde{V}$ and $\widetilde{I}$ in the complex plane at a time $\pi/(4\omega)$. Does the current lead the voltage or lag it? How can you tell?
- Sketch the driving voltage and the current through the voltage source as a function of time. Does the current lead the voltage or lag it? How can you tell?
- Assume that $1/(\omega C) < \omega L$. What happens to your answers in parts 4 and 5?
- Critique the phasor and time domain representations. Which makes more sense to you to understand leading and lagging? Do you see any problems with using the “rules” we discussed in class (i.e., “leading means peaks before” and “lagging means peaks after”)? Is there anything you need to be careful about when using those rules?
- Find an experiment where knowing about leading and lagging current matters. Briefly summarize it.
2. Parallel RLC Circuit
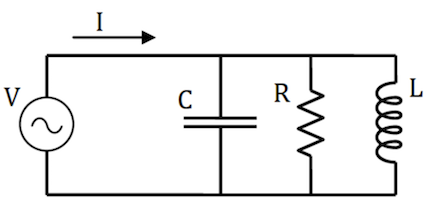
This parallel RLC circuit is driven by an AC voltage $V=V_0 \cos(\omega t)$.
- What is the total complex impedance that the voltage source sees? Write the answer in the format $Z = Z e^{i\theta}$; i.e., give the magnitude and phase angle of the impedance. (Hint: It is simplest to begin by computing the magnitude and phase of $1/Z$.)
- Using complex analysis (the phasor method) solve for the “true” current $I_{true}$ through the voltage source $I_{true} = Re\left[I\right]$.
- Using a jupyter notebook, graph the magnitude of the current I vs. frequency. At what frequency is the current at an extremum?
You will turn your notebook in using your GitHub repository.
3. A Terminated Line Current
Consider a straight wire that runs from $z=-\infty$ to $z=0$ that has a steady current flowing $I$. At the location where the wire terminates, charge builds up, $Q(t)$. The goal of this problem is to find the magnetic field everywhere.
- Determine the electric field produced by the charge buildup.
- Determine the displacement current in terms of $I$. Think about how conservation of charge tells you about the relationship between $Q(t)$ and $I$.
- In part 2, you should have found a spherically symmetric result. Using Ampere’s Law with a hemispherical cap (circular loop around the charge in the plane perpendicular to the long wire) in the positive z-direction, find the integral of $\oint \mathbf{B} \cdot d\mathbf{l}$.
- Using Ampere’s Law with a hemispherical cap (circular loop around the charge in the plane perpendicular to the long wire) in the negative z-direction, find the integral of $\oint \mathbf{B} \cdot d\mathbf{l}$. Does this agree with part 3?
- Find the magnetic field everywhere in the plane (z=0) that intersects the line current.
- Bonus: Find the resulting magnetic field everywhere in space. Did you remember the long wire? What loop and surfaces are you using to determine the magnetic field? Sketch a picture that makes it clear.
4. A Terminated Surface Current
Consider a current with surface density $\mathbf{K} = -\vert K\vert\hat{x}$ that flows in a half-plane ($z=0$, $x>0$). The current results in an accumulation of charge on the line boundary of the half-plane. The goal of this problem is to find the magnetic field everywhere.
- Determine the electric field produced by the charge buildup, for now you may use $\lambda(t)$.
- Determine the displacement current in terms of $\mathbf{K}$. Think about how conservation of charge tells you about the relationship between $\lambda(t)$ and $\mathbf{K}$.
- Bonus: Find the resulting magnetic field everywhere in space. Did you remember the surface current? What loop and surfaces are you using to determine the magnetic field? Sketch a picture that makes it clear.
5. Project Problem - Building your paper III
Last week, you built on your paper by adding to the summary that you wrote; filling it out with additional detail and responding to the feedback that you received. Like last week, you will be building and working towards finalizing a full draft of your paper. It doesn’t have to be entirely done, that’s what the next two weeks are for, but it should be getting close. Again, work to write something that is coherent and tells a complete story. Make sure that you think about the feedback that you received last week and the week before. Make sure you check it for spelling and grammar. This is your chance to really push out a good draft of your paper and get feedback from me before turning in the final project in next week.
For this week, you should start thinking about:
- What are the difficulties or successes connecting theory and experiment?
- How can I dig deeper and explain in more detail what I’ve learned from the previous papers and the ones I’m reading currently?
- What kind of feedback did I get about my previous summary and how do I improve on what I’ve done?
My aim for scaffolding your paper writing with these homework problems is to make the eventual paper that you turn in less stressful and to give you a chance to get feedback from me early on.
You will turn this question in using your GitHub repository.