Homework 5 (Due. Feb 15)
1. An LC circuit
Consider a circuit with a capacitor and an inductor only. Suppose this LC circuit starts at time $t=0$ with charge $Q_0$ on the capacitor and zero initial current.
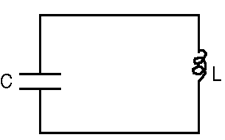
- Write down the differential equation for charge on the capacitor as a function of time and solve for $Q(t)$.
- Find the voltage across the capacitor, the voltage across the inductor, energy stored in the capacitor, and energy stored in the inductor, as functions of time.
- Describe in words the energy flow in the circuit. Show that the total electromagnetic energy in the circuit is conserved.
- Describe an analogous mechanical system (i.e. one that obeys the same differential equation) and provide “translations” between all important variables.
2. An AC circuit
In the circuit shown in the figure, the power supply provides an EMF of $V_0 \cos \omega t$.
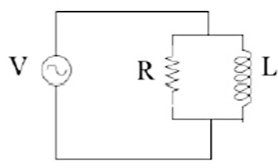
- Find the current through the power supply as a function of time after all the transients have died away. Use the method of “phasors”!
- How does your answer behave in the limits $\omega \rightarrow 0$ and $\omega \rightarrow \infty$? Make sense of these limits, given the characteristics of an inductor.
3. Another AC Circuit
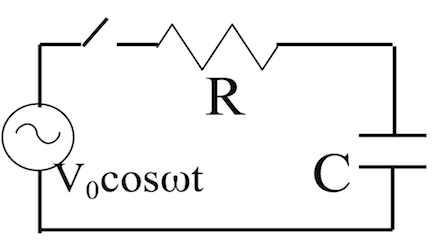
If you drive the RC circuit shown with an AC source $V = V_0 \cos(\omega t)$, closing the switch at t=0, the resulting current is:
\[I(t) = \dfrac{V_0}{\sqrt{R^2+1/C^2\omega^2}}\cos(\omega t + \phi) + \dfrac{V_0}{R}\dfrac{1}{1+R^2C^2\omega^2}e^{-t/RC},\]with $\phi = \tan^{-1}(1/RC\omega).$
You do not have to derive that formula! (though you’re welcome to, I think it’s good practice) Instead, here are some questions about interpreting this result. (In all these questions, where we say “response”, I generally mean “the amplitude of current”)
- What is the time constant for this circuit? (Can you just “spot it”? No calculation needed!) Briefly, how do you interpret it physically, what is it telling you? How would you make it longer?
- How do you read off from that formula the “long time” response? (Again, no calculation needed, can you just “spot it”?) Describe this long term response in words, what is physically happening?
- After a long time, is the current “leading” or “lagging” the source voltage? (Again, no calculation needed, can you just “see” the answer from the formula?)
- Which leads to a stronger response of this circuit after a long time: low or high driver frequency? (Briefly, does this make physical sense to you, given this circuit?)
4. Signal Filtering
The following LR circuit is driven by an AC voltage source $V_{in} = V_0 \cos(\omega t)$. It can be regarded as a filter that changes $V_{in}$ into $V_{out}$.
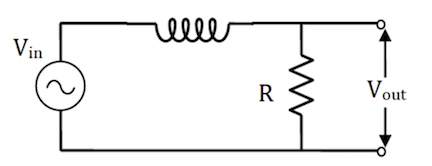
- Using complex analysis (the phasor method) solve for the “true” current $I_{true}$ in this circuit: $I_{true} = Re[I]$.
- Solve for the complex ratio $V_{out} / V_{in}$ (give the magnitude and phase of this ratio) as a function of frequency. Check that your answer makes sense in the limits $\omega \rightarrow 0$ and $\omega \rightarrow \infty$.
- Using a jupyter notebook, graph the magnitude of $V_{out} / V_{in}$ vs. frequency. How would you describe this filter? Is it a high-pass filter? Low-pass? Band-pass?
- BONUS (10 pts): Check your result in part 3 by considering an input signal that is a square wave, which can be constructed from a sum of sinusoidal functions. In the same jupyter notebook, graph $V_{in}$ as a function of time. Then determine $V_{out}$ as a function of time and plot it. Think before doing a lot of mathematics! All the equations are linear, so if the input square wave is constructed from the sum of sinusoidal functions, what does the output look like?
Hint: If you use a loop you should start to see the effects more easily as you can keep as many terms as you want.
You will turn your notebook in using GitHub repository.
5. Project Problem - Building your paper II
Last week, you summarized your background research so far. I am looking for about 3-4 additional paragraphs on what you have learned so far; you should keep reading papers, so you should 1-2 additional references in this summary. Here, you should be adding to the summary that you wrote last week; filling it out with additional detail and responding to the feedback that you received. Like last week, think about writing this as part of your eventual paper, so work to write something that is coherent and tells a complete story. Make sure you check it for spelling and grammar. This is your chance to make headway on the eventual project that you will turn in soon.
For this week, you should start thinking about:
- What are the predictions of the models that describe my phenomenon?
- What mathematical tools are used to make these predictions?
- How can I dig deeper and explain in more detail what I’ve learned from the previous papers and the ones I’m reading currently?
- What kind of feedback did I get about my previous summary and how do I improve on what I’ve done?
You will turn this question in using your GitHub repository