1. Homopolar Motor

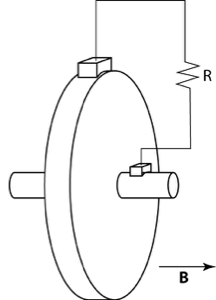
Michael Faraday came up with a relatively simple DC generator called a homopolar generator (shown above). A conducting wheel of diameter $D$ rotates with angular velocity $\omega$ in a uniform B-field oriented along the wheel axis. Sliding contacts make an electrical connection between the center of the wheel and the edge, as shown, and an EMF is induced across a load resistance $R$.

1. Show that the power dissipated in the resistor is $??\omega^2B^2D^4/R$, (where the “??” is some numerical constant out front. Is it 1, 0.5, $\pi$,…?)
2. How fast would a 1 m diameter generator in a 0.2 Tesla magnetic field have to rotate to produce an EMF of 120 V? (answer in Hz, please).

2. Eddy current brake:

An electromagnetic “eddy current brake” consists of a solid spinning wheel of conductivity $\sigma$ and thickness $d$. A uniform field $B_0$ is applied perpendicular to the surface of the wheel over a small area $A$ located a distance $s$ from the axis.

1. Show that the torque on this disk is given (very approximately) by $\tau = \sigma \omega B^2 s^2 A d$.
2. Estimate how high $B_0$ should be for this kind of brake to be functional as a car brake, given a magnet size of 20 $\mathrm{cm}^2$ per brake. (“Estimate” here means just that – make some reasonable guesses about the various parameters you need. Think about real cars in the real world! Order of magnitude is what we’re after, don’t fuss about factors of 2 or 3) Do you foresee any problem as the car slows down?

3. Moving in a Time-Varying Field

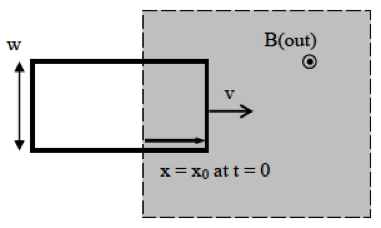
A rectangular loop of metal wire, of width $w$, moving with constant speed $v$, is entering a region of uniform B-field. The B-field is out of the page and is increasing at a constant rate $B=B_0 + \alpha t$, where $B_0$ and $\alpha$ are positive constants. At t = 0, the right edge of the loop is a distance $x_0$ into the field, as shown. Note that the EMF around the loop has two different causes: the motion of the loop and the changing of the B-field.

1. Derive an expression for the magnitude of the EMF around the loop as a function of time, while the loop is entering the field.
2. Is the induced current in the loop clockwise, counterclockwise (or impossible to determine without knowing the values of $v$ and $a$?) Explain.
3. Also, explicitly check that your answer to part 1 makes sense by (i) checking units and (ii) considering the two cases $v = 0$ and $\alpha = 0$. Explain how these limits give answers you might expect.
4. Using a jupyter notebook, graph the expression for the EMF as a function of time for different ranges of $\alpha$. By ranges here, I mean different orders of magnitude for $\alpha$. This technique can be used to see if there is qualitatively different behavior when parameters change. Is there? What about for different ranges of $v$?

You will turn part 4 in using your GitHub repository

4. Falling Metal Loop

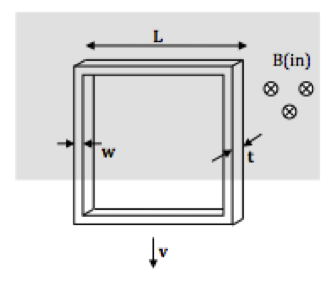
A square metal loop is released from rest and falls straight down. The loop is between the poles of a magnet with uniform B field, and initially, the top of the loop is inside the field and the bottom of the loop is outside the field. The metal has mass density $\rho_m$ and electrical resistivity $\rho_e$. The loop has edge length $L$, and is made of a rectangular wire with very small transverse dimensions $w$ and $t$.

1. What is the EMF around the loop in terms of the downward speed $v$ of the loop? Assume the loop reaches terminal velocity before it passes entirely outside the field, and derive an expression for the terminal speed of the loop. Do some qualitative sensemaking/sanity checks: Units? Does the functional dependence on the various variables seem reasonable? (Nothing quantitative, just e.g. arguing that $v_{term}$ should be bigger if $g$ is bigger - it’s pulled harder by gravity!)
2. Show that (when traveling at $v_{term}$) the rate at which thermal energy is generated in the metal ($P_{thermal}$) is equal to the rate at which gravity does work on the loop ($P_{grav}). Briefly, why must they be equal?
3. At t = 0, the loop starts at rest. Use $F_{net} = ma$ to write down a differential equation for the speed $v$ of the loop. Then, solve for the speed $v$ as a function of time. You should find that the speed approaches the terminal speed exponentially – sketch $v(t)$. What is the time constant for this exponential motion? If the metal is aluminum, and $B$ is, say, 0.2 T, what is the numerical value of the time constant? (Hint: I claim the values of L, w, t don’t matter. Show us why not!)

5. Project Problem - Continuing your annotated bibliography

(Actually due on Friday)

Last week, you started an annotated bibliography, a detailed summary of each of the 2 articles you read. Make sure you read over your feedback carefully and make any adjustments that are requested.

This week you will continue that work by adding to your bibliography by writing a detailed summary of at least 2 additional articles. You should also review the feedback that you received and adjust the summaries of the prior two articles as well as the current two to more well aligned with the feedback. A perfect score on this question will reflect the quality of the adjustments that you made as a result of the feedback.

Below are the instructions, which are (mostly) repeated from last week:

For this week, read and summarize 2 additional journal articles. While working through each paper think about the following questions to guide your summary of each: What does the paper say about your phenomenon? How are the theoretical models constructed? What assumptions and approximations are being made? What are the predictions and implications? What more do you need to know to understand this article? For this first summary, I expect you to write 2-3 paragraphs per article that you summarize. You may include equations and figures, but they do not count towards the total number of paragraphs.

You will turn this in using your GitHub repository