Homework 2 (Due. Jan 18)
1. An Electric Field that We Will Revisit
Suppose an electric field in a region of space is given by
\[\mathbf{E} = \dfrac{B_0}{2 \tau}\left(-y\hat{\mathbf{x}}+x\hat{\mathbf{y}}\right)\]where $\tau$ is a constant with units of time and $B_0$ is some given constant.
- What are the units of the constant $B_0$?
- Sketch the E-field in the x–y plane (by hand).
- Calculate the closed line integral $\oint_L \mathbf{E} \cdot d\mathbf{l}$ where $L$ is a circle of radius $R$, parallel to the $x–y$ plane, centered at $\langle 0,0,z_0 \rangle$. Integrate counterclockwise as viewed from “above”. (i.e viewed from $+z$)
- Calculate the closed line integral equation again, this time where $L$ is a rectangle (sides of length $a$ and $b$, centered around the origin) oriented parallel to the $x–y$ plane. (Again, integrate counterclockwise as viewed from “above”) Clearly describe in words how the value of integral here and in part 3, depends on $B_0/\tau$ and the geometry of $L$.
- Calculate $\nabla \times \mathbf{E}$ and describe the resulting vector field in words. Show that the closed line integral values in part 3 and 4 are equal to the corresponding surface integrals of $\nabla \times \mathbf{E}$. Relate this to Stokes’ theorem!
- Determine the scalar potential that gives equation the above electric field (or explain why no such potential exists.) Finally - describe how you could use such a static electric field to make a lot of money and save the world. Does the electric field in this problem violate any of Maxwell’s equation for a static situation? Does this “mathematical exercise” strike you as a physically unrealistic problem? We’ll come back to this field soon, there’s more to it than meets the eye!
2. Magnetic Resonance Imagers
Example 5.6 in Griffiths gives the magnetic field along the axis of a single circular loop of wire of radius $a$, carrying a current $I$. In this problem, consider a solenoid, which is effectively many such circular loops stacked up to make a cylinder.
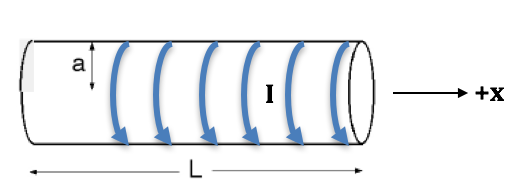
- Let’s design a cylindrical solenoid for a magnetic resonance imager capable of imaging an adult human. Assume the solenoid has radius $a$, length $L$, is wrapped with $n$ turns per unit length of wire, and the wire carries current $I$. Derive the functional form of the field, $\mathbf{B}(x)$ along the center line of the device, by integrating the contributions of a set of infinitesimal current loops. (I would choose $x=0$ to be at the very middle of the solenoid.)
- Explicitly show that your result approaches the “known” result (e.g. Example 5.9 of Griffiths) if the solenoid becomes infinite.
- Choosing appropriate (physically sensible) values for the length $L$ and radius $a$ (discuss your choices!), sketch a simple plot of the magnetic field vs. position (just along the central, x-axis). Please make your horizontal axis be the “dimensionless variable” $x/L$, and your vertical axis be the “dimensionless magnetic field” $B/(\mu_0 n I)$.
- Verify graphically that for $L \gg a$ the field near the center of the solenoid is nearly constant and is nearly equal to the field inside an infinite solenoid.
3. The Magnetic Vector Potential
Suppose the magnetic vector potential in a region of space is given by:
\[\mathbf{A} = A_0 exp\left(-\frac{x^2+y^2}{a^2}\right)\hat{\mathbf{z}}\]- What are the units of the given constants $a$ and $A_0$?
- Determine the B-field from this vector potential, $\mathbf{B} = \nabla \times \mathbf{A}$. (Note: $\mathbf{A}$ is given in Cartesian coordinates - what coordinate system would make your calculations easier? Use that!)
- Determine the current density, $\mathbf{J}$, from the B-field. (Use an appropriate Maxwell’s eqn!)
- Separately sketch the vector field $\mathbf{A}$, the magnetic field $\mathbf{B}$, and the current density $\mathbf{J}$ you found above, using any representation you feel conveys the most useful information. Briefly, for EACH of the three plots, also use English words to describe what they look like. (If your representation “hides” information, state what that is.)
- Integrate the current density to show that the total current flowing through any infinite plane parallel to the $x-y$ plane is zero. Then, give a simple argument (without doing any formal integral) why you might have known before calculating that this must be the case.
- Calculate the divergence of the current density J. What does the value of the divergence imply, in terms of Griffiths: Equation (5.29)? Does this set of fields strike you as an unphysical math exercise, or can you imagine some physical system or device, which might be (approximately) represented by this problem?
4. Microscopic Description of Current
- We frequently use the relation for current density $\mathbf{J} = nq\mathbf{v}$, where $n$ is the number density (number per volume) of charge carriers, $q$ is the charge of each carrier, and $v$ is the average velocity of the charge carriers: the “drift” velocity. This is not the DEFINITION of J, it is a derived expression - briefly but clearly (in your own words) summarize the chain of arguments in its derivation. (A little sketch helps! You might go back to Griffiths 5.1.3)
- In most metals, there is roughly one conduction electron per atom. Consider a copper wire (1 mm diameter) carrying a current of 10 A (these numbers are typical of home wiring) Compute the drift velocity of electrons in this wire. (Is it surprising? Comment, briefly.)
- If I stretch a given piece of copper wire, making it 0.1% longer, how much would this (roughly) change the resistance from end to end? (What assumptions are you making?)
- Suppose I connect two 1-mm diameter wires end to end, made of different materials, copper to gold. When 10 A flows through the system, a thin layer of charge appears at the boundary. Estimate the total charge that has accumulated at the boundary. What is the sign of the accumulated charge? What determines this sign? (Note: Griffiths Table 7.1 may be helpful here, and of course our usual boundary conditions, back in Griffiths Chapter 2.3.5)
5. Speherical resistors
Resistors can take a number of forms, consider one constructed from two concentric metal spheres with a conducitng material filling the space between them. The spheres have radii $R_1$ and $R_2$ and the material has conductivity $\sigma$.
- Show that the potential difference across them is a constant: $V$, that global statement of steady state current holds. That is, what is the current for any distance $r$ from the inner sphere?
- What happens with the local statement, $\nabla \cdot \mathbf{J} = \partial \rho / \partial t$? Comment on any pecularities you find.
- Determine the resistance between the shells.
6. Investigating the Electric Field in a Wire
This problem includes a Jupyter notebook that will compute the electric field of a charged ring along its central axis. Your job is to modify this code to investigate the profile of the electric field inside a wire. Recall that the excess charge on the surface of the wire generates the electric field that moves charges in the wire. This charge distribution is gradated (i.e., it slowly changes sign as you move from the anode to cathode).
To do this investigation, you will need to perform two tasks:
- Compute and display the electric field at several locations inside the loop of the ring (i.e., in the plane of the ring) to observe the distribution of the field when only one ring is present, and
- Add a number of additional rings (forming a tube or rather a “thick” wire), and recompute the electric field at the same locations.
Notice for task 2, you will need to add rings on either side of the initial ring with gradated surface charge (i.e., the charge of each ring will change a little as you move away from the central ring).
You will turn this in using your GitHub repository.
7. Project Problem - Starting an annotated bibliography
Last week, you identified an area of physics that you were interested in investigating further. Make sure you read over your feedback carefully and make any adjustments that are requested.
Starting from your proposed list of articles, you will begin to construct an annotated bibliography. In research, it’s often useful to write a short summary of your own about the articles that you read. That way you don’t have to return to the article entirely to make sense of what you know. This is a living document that gets added to and refined as you read more literature.
For this week, read and summarize 2 of the 4 relevant journal articles. While working through each paper think about the following questions to guide your summary of each: What does the paper say about your phenomenon? How are the theoretical models constructed? What assumptions and approximations are being made? What are the predictions and implications? What more do you need to know to understand this article? For this first summary, I expect you to write 2-3 paragraphs per article that you summarize. You may include equations and figures, but they do not count towards the total number of paragraphs.
You will turn this in using your GitHub repository.