25 Oct 23 - Notes: Solutions to The Wave Equation#

The wave equation is a partial differential equation that describes how waves propagate (they are fundamentally a disturbance of a medium) in space and time. The general wave equations is:

\[\nabla^2 u(\mathbf{r},t) = \frac{1}{v^2} \frac{\partial^2 u(\mathbf{r},t)}{\partial t^2}\]

where \(u(\mathbf{r},t)\) is the displacement of the wave at position \(\mathbf{r}\) and time \(t\) and \(v\) is the speed of the wave in the medium. Now we typically don’t solve this problem in general, like most PDEs, we need a context in which to work on the problem. Moreover, that wave equation is 4 dimensional and we really are going to have a hard time with intuition if we focus on that. Let’s instead consider the 1D wave equations:

\[\frac{\partial^2 u(x,t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 u(x,t)}{\partial t^2}\]

where \(u(x,t)\) is the displacement of the wave at position \(x\) and time \(t\) and \(v\) is the speed of the wave in the medium. This is a much more tractable problem.

It is comment to rewrite this problem using the D’Alembert operator \(\square\):

\[\square u(x,t) = 0\]

where \(\square\) is defined as:

\[\square = \frac{\partial^2}{\partial x^2} - \frac{1}{v^2} \frac{\partial^2}{\partial t^2}\]

Traveling Waves#

Through this operator and proposed change of variables: \(\eta = x - vt\) (movement to the right) and \(\xi = x + vt\) (movement to the left) we can show that the general solution to the 1D wave equation are just functions of those variables:

\[u(x,t) = f(\eta) + g(\xi) = f(x-vt) + g(x+vt)\]

where \(f\) and \(g\) are arbitrary functions. This is a very powerful result; the solution to the wave equation is a function of a given shape (\(f(x)\) or \(g(x)\)) that travels to the right and/or left; if both, they superpose in space and time. We will use a special case of these solutions sinusoidal traveling waves as they demonstrate the key features of waves; but also behave nicely (in the mathematical sense) in the context of the wave equation.

Sinusoidal Traveling Waves#

A sinusoidal traveling wave is a infinite wave that has a sinusoidal shape (\(\sin\) or \(\cos\)). It is a solution to the wave equation (notice it is not a separable solution):

\[u(x,t) = A \sin(kx - \omega t + \phi)\]

where \(A\) is the amplitude of the wave, \(k\) is the wave number, \(\omega\) is the angular frequency, and \(\phi\) is the phase. This wave exists for all space and time, so it is a model of a real wave. We often use series of these waves to build up shorter wave packets. Like below is a sum of travelling waves with different wave numbers and angular frequencies to produce a packet. It can be analyzed simply because it’s a sum of sinusoidal waves.

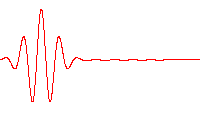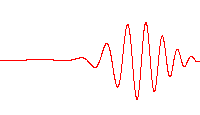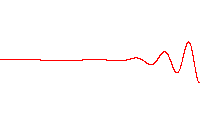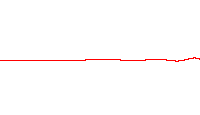
Wave packet

In the traveling wave solution, the wave number and angular frequency are related to the speed of the wave in the medium:

\[v = \frac{\omega}{k}\]

Notice that this is a right traveling wave. We can also write a left traveling wave:

\[u(x,t) = A \sin(kx + \omega t + \phi)\]

In general the 1D wave is a superposition of these two waves:

\[u(x,t) = A_1 \sin(kx - \omega t + \phi_1) + A_2 \sin(kx + \omega t + \phi_2)\]

where the amplitudes and phases are set by the problem. Below we see how this general solution satisfies the wave equation.

\[\frac{\partial^2 u(x,t)}{\partial x^2} = -k^2 A_1 \sin(kx - \omega t + \phi_1) - k^2 A_2 \sin(kx + \omega t + \phi_2)\]
\[\frac{\partial^2 u(x,t)}{\partial t^2} = -\omega^2 A_1 \sin(kx - \omega t + \phi_1) - \omega^2 A_2 \sin(kx + \omega t + \phi_2)\]

Pop into the wave equation:

\[-k^2 A_1 \sin(kx - \omega t + \phi_1) - k^2 A_2 \sin(kx + \omega t + \phi_2) = \frac{1}{v^2} \left(-\omega^2 A_1 \sin(kx - \omega t + \phi_1) - \omega^2 A_2 \sin(kx + \omega t + \phi_2)\right)\]

Collect terms and then divide by the common factor:

\[-k^2\left(A_1 \sin(kx - \omega t + \phi_1) + A_2 \sin(kx + \omega t + \phi_2)\right) = -\frac{\omega^2}{v^2} \left(A_1 \sin(kx - \omega t + \phi_1) + A_2 \sin(kx + \omega t + \phi_2)\right)\]

For nonzero solutions:

\[-k^2 = -\frac{\omega^2}{v^2} \rightarrow v = \pm \frac{\omega}{k}\]

Left or right sinusoidal traveling waves solve the wave equation as long as the speed of the wave is related to the frequency and wave number as indicated.

Diffraction#

A critical result of superposition is the interference of waves. For example two waves in a pool below interfere to produce a wave that travels outward.

Interference

It turns out these kinds of interference patterns are very useful. Because with models of waves, we can predict their pattern and shape. Moreover, they can serve as instruments to investigate systems. For example, x-ray diffraction is a common and widely used tool to determine the shape and structure of matter. A number of folks have earned Nobel prizes for their work on X-ray diffraction and its applications. We will develop the mathematics of diffraction later, but Parth G has a nice video on the topic of Diffraction.

Diffraction

Single Photo Diffraction#

One of the most intersting things we have found in recent years is single particle diffraction. In fact, this was observed macroscopically in pilot wave hydrodynamics by a French research group. We have found that interference patterns can build up in single photo experiments. The video below shows a set up that demonstrates this.

Single Particle Diffraction

Resources#

Much of what we are discussing about waves appears in the following sets of notes: