10 Oct 23 - Activity: Matching Boundary Conditions and Plotting the Potential#

Azimuthally Symmetric Solutions#

As we saw, azimuthally symmetric solutions, the electric potential is independent of \(\phi\) and the solutions are of the form:

\[V(r,\theta) = \sum_{n=0}^\infty \sum_{l=0}^\infty \left(A_{nl} r^n + \frac{B_{nl}}{r^{n+1}}\right) P_l(\cos\theta)\]

where \(P_l(\cos\theta)\) are the Legendre polynomials. The coefficients \(A_{nl}\) and \(B_{nl}\) are determined by the boundary conditions. We will practice solving for these coefficients in this activity.

✅ Do this

Sphere of constant surface potential#

Consider a sphere of with a radius \(a\). If the potential on the surface is \(V_0\), what is the potential inside and outside the sphere?

  1. Consider the radial solutions (what doesn’t blow up?)

  2. Consider the polar angle solutions, what has to be true? What does that say about terms with \(l>0\)?

  3. Write down the solution inside and outside the sphere.

  4. Make a heat map plot (in \(x\) and \(y\)) of the potential inside and outside the sphere. You can set \(a=1\) and \(V_0=1\) if that helps.

## your code here

✅ Do this

Sphere of variable potential#

Consider a sphere of with a radius \(a\). If the potential on the surface is \(V(\theta)\), what is the potential inside and outside the sphere?

  1. Consider the radial solutions (what doesn’t blow up?)

  2. Consider the polar angle solutions, what has to be true? Can you say anything about them?

  3. What if \(V(\theta) = V_0 \cos(\theta)\)? What is the potential inside and outside the sphere?

A thick spherical shell#

Suppose you have a spherical shell of inner radius \(a\) and outer radius \(b\), and you know the electric potential on the inner (\(V(a,\theta) = V_a(\theta)\)) and outer (\(V(b,\theta) = V_b(\theta)\)) surfaces. You want to find the electric potential \(V(r,\theta)\) inside the hole (\(r<a\)) and outside the shell (\(r>b\)).

Let’s allow:

\[V_a(\theta) = V_{a0} + V_{a1} \cos(\theta)\]
\[V_b(\theta) = V_{b0} + V_{b1} \cos(\theta)\]

  1. What is the general solution? (all three regions)

  2. What are the boundary conditions for \(r\)?

  3. What terms are left in the general solutions?

  4. Find the unique solution for \(V(r,\theta)\) inside the hole (\(r<a\)) and outside the shell (\(r>b\)).

What do you do in the case of \(V_a(\theta) = f(\theta)\) and \(V_b(\theta) = g(\theta)\) - generic functions?

Example of Polarization#

✅ Do this

Put a metal sphere of radius \(a\) in a uniform electric field \(\vec{E} = E_0 \hat{z}\).

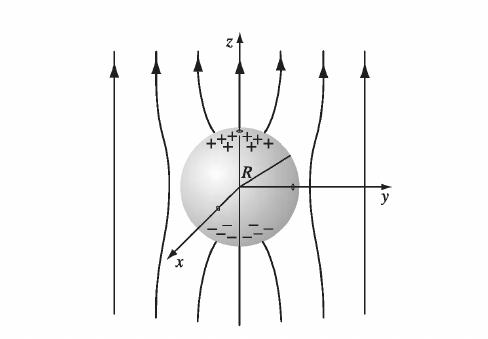
Sphere in a uniform electric field

What is the potential inside and outside the sphere?

  1. Draw the picture and write down the boundary conditions. What is the potential everywhere on a metal?

  2. What general solution do you need to use? How do you know?

  3. What are the boundary conditions for the radial solutions? The polar angle solutions?

  4. Match your boundary conditions to your general solution. What is the potential inside and outside the sphere?

  5. Make a heat map plot (in \(x\) and \(y\)) of the potential inside and outside the sphere. You can set \(a=1\) and \(E_0=1\) if that helps.

  6. (challenge) Find the polarization charge density on the surface of the sphere. What is the total charge on the sphere?

## your code here