Day 28 - Hallmarks of Chaos

Day 28 - Hallmarks of Chaos#

bg right width:600px

Conceptualizing the Lyapunov Exponent#

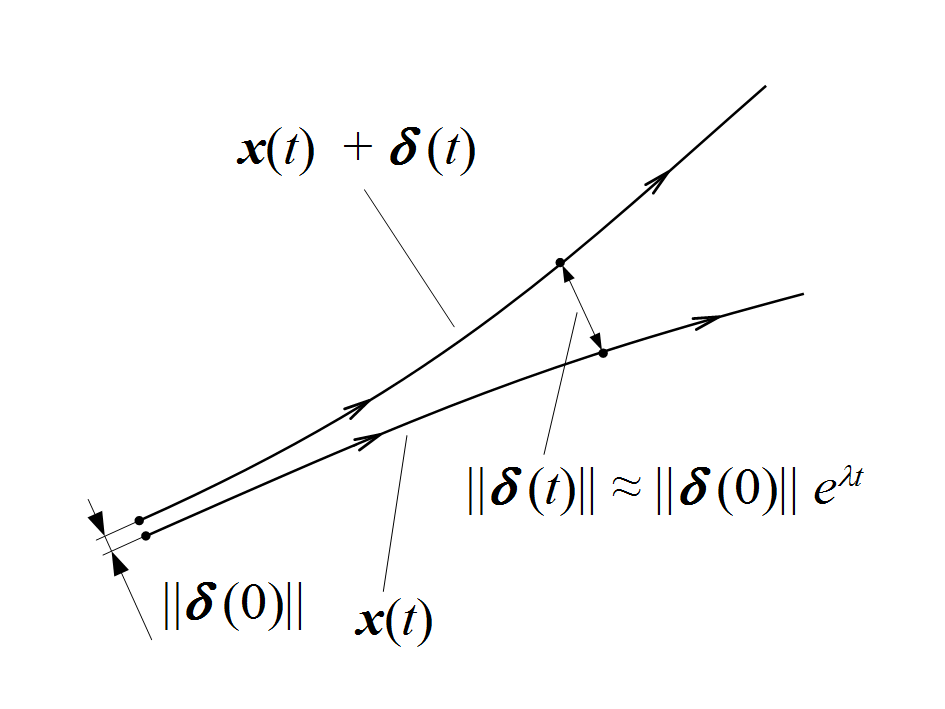
Trajectories diverge exponentially in time

Announcements#

  • Midterm 1 is graded

  • Homework 7 is due Friday

    • No homework next week

  • Midterm 2 will be assigned next Monday (due 18 April)

    • Second project check-in

Seminars This Week#

WEDNESDAY, March 26, 2025#

  • Astronomy Seminar, 1:30 pm, 1400 BPS, Bryan Terrazas, Oberlin College, Galaxy evolution and feedback modeling

  • FRIB Nuclear Science Seminar, 3:30pm., FRIB 1300 Auditorium, Dr. Jacklyn Gates of Lawrence Berkeley National Laboratory, Toward Pursuing New Superheavy Elements

Seminars This Week#

THURSDAY, March 27, 2025#

  • Special FRIB/MSU Nuclear Science Seminar with Colloquium, 3:30 pm, 1415 BPS, Mandie Gehring, LANL, Measuring Intense X-ray Spectra and an Overview of Space Research at Los Alamos National Laboratory

FRIDAY, March 28, 2025#

  • IReNA Online Seminar, 2:00 pm, In Person and Zoom, FRIB 2025 Nuclear Conference Room, Jordi José, Technical University of Catalonia, UPC (Barcelona, Spain), Classical novae at the crossroads of nuclear physics, astrophysics and cosmochemistry

Hallmarks of a Classically Chaotic System#

  1. Deterministic

  2. Sensitive to Initial Conditions

  3. Non-periodic Behavior

  4. Strange Attractors

  5. Parameter Sensitivity

  6. (Sometimes) Periodic Behavior

Limit Cycle#

A limit cycle is a closed trajectory in phase space that is an attractor for a dynamical system.

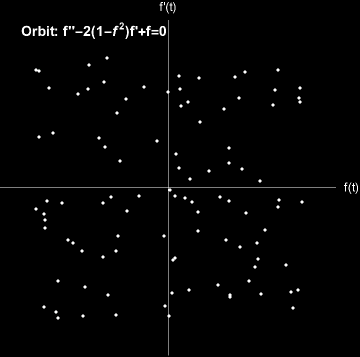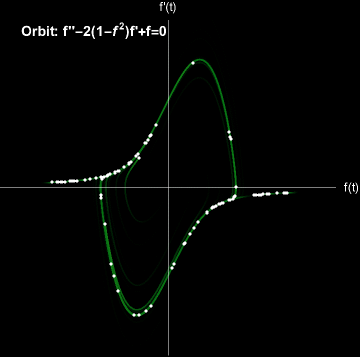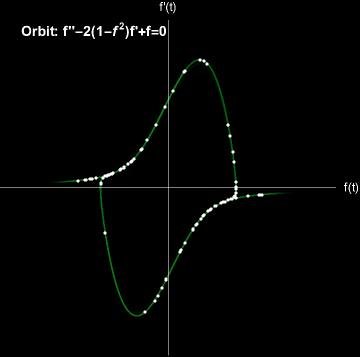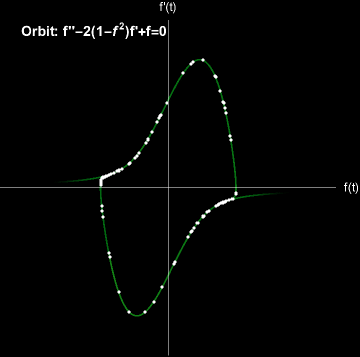
bg right

The Van der Pol Oscillator exhibits a limit cycle.

\[\ddot{x} - \mu (1 - x^2) \dot{x} + x = 0\]

Random initial conditions converge to a limit cycle. Modeled with \(\mu=2\).

The Lyapunov Exponent#

bg right width:700px

\(\vec{\delta}(t)\) is the separation vector between two trajectories in phase space \(\vec{\delta}(t) = \vec{x}_2(t) - \vec{x}_1(t)\).

Do trajectories diverge exponentially in time, \(|\vec{\delta}(t)| \approx |\vec{\delta}(0)| e^{\lambda t}\)?

Each phase coordinate can change at a different rate: \(\vec{\lambda} = \langle \lambda_1, \lambda_2, \dots, \lambda_n \rangle\).

Largest \(\lambda_i > 0\)? Chaotic system.

Strange Attractors#

A strange attractor is a set of points in phase space that a chaotic system approaches.

Chen Attractor

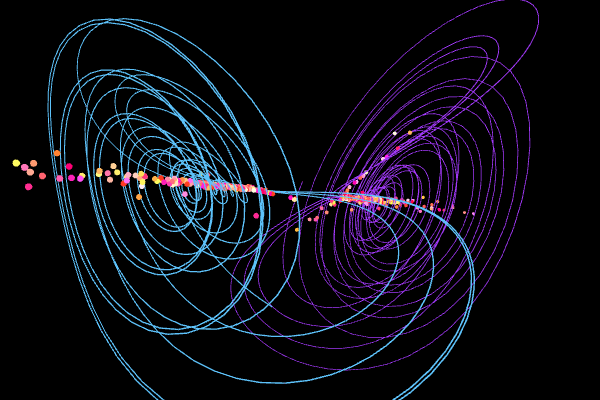
Chen Attractor bg left

\[\dot{x} = \alpha x-yz\]
\[\dot{y} = \beta y + xz\]
\[\dot{z} = \gamma z + xy/3\]

\(\alpha=5\), \(\beta=-10\), \(\gamma=-0.38\).

Interactive 3D Model

Example 1: Duffing Equation#

\[\ddot{x} + \beta \dot{x} + \alpha x + \gamma x^3 = F_0 \cos(\omega t)\]

width:1200px

Exhibits Periodic and Chaotic Behavior

Illustrates period doubling bifurcations as route to chaos

Example 2: Lorenz System#

\[\dot{x} = \sigma (y - x)\]
\[\dot{y} = x (\rho - z) - y\]
\[\dot{z} = x y - \beta z\]

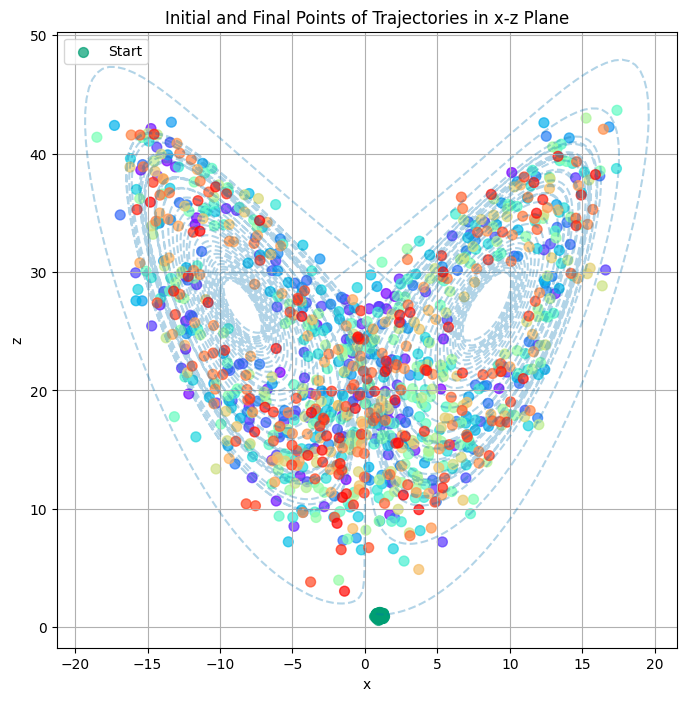
bg right width:600px

Exhibits sensitive dependence on initial conditions Demonstrates the concept of a strange attractor