Day 23 - Help Session

---

Announcements

• Midterm 1 is still being graded

  • Re: Problem 2 and 4 \(\rightarrow\) HOLY CRAP YOU ALL ARE AMAZING 🎉🎉🎉

• Homework 5 is due tonight

• Homework 6 is due next Friday

---

Reminders

We solved the damped harmonic oscillator equation:

\[\ddot{x} + 2 \beta \dot{x} + \omega_0^2 x = 0\]

We chose a solution (ansatz) of the form

\[x(t) = C_1 e^{r t} + C_2 e^{r t}\]

and computed the roots of the characteristic equation:

\[r^2 + 2 \beta r + \omega_0^2 = 0\]

We found the roots to be:

\[r = -\beta \pm \sqrt{\beta^2 - \omega_0^2}\]

---

Weak Damping

We found that when \(\beta^2 < \omega_0^2\), the roots are complex:

\[r = -\beta \pm i \sqrt{\omega_0^2 - \beta^2}\]

This means that the solution is oscillatory:

\[x(t) = e^{-\beta t} \left( C_1 \cos(\sqrt{\omega_0^2 - \beta^2} t) + C_2 \sin(\sqrt{\omega_0^2 - \beta^2} t) \right)\]

The solution is a damped oscillation with frequency \(\omega_1 = \sqrt{\omega_0^2 - \beta^2}\).

---

Strong Damping

When \(\beta^2 > \omega_0^2\), the roots are real:

\[r = -\beta \pm \sqrt{\beta^2 - \omega_0^2}\]

This means that the solution is not oscillatory: $\(x(t) = C_1 e^{r_1 t} + C_2 e^{r_2 t}\)\( where \)r_1 = -\beta + \sqrt{\beta^2 - \omega_0^2} < 0\( and \)r_2 = -\beta - \sqrt{\beta^2 - \omega_0^2} < 0$.

The solution is the sum of two exponentials with different decay rates.

---

Critical Damping

When \(\beta^2 = \omega_0^2\), the roots are real and equal (repeated roots): $\(r = -\beta\)$

This means that the solution is not oscillatory, but also that our ansatz is not sufficient. The correct form of the solution is:

\[x(t) = (C_1 + C_2 t) e^{-\beta t}\]

In most cases, we will work with weak damping.

---

Exercise 4, baby bifurcations

The apparatus to the right is a massless wheel of radius \(R\) that is mounted to a frictionless axle. A small, dense piece of clay with mass \(M\) is glued to edge of the wheel as shown. Another mass \(m\) hangs from a massless string that is wrapped around the wheel. We can assume the string is inextensible and does not slip, and the system is in a uniform gravitational field.

---

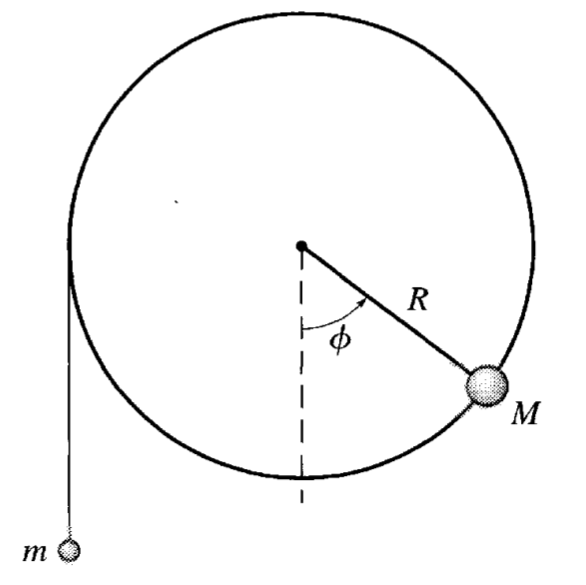
Exercise 4, baby bifurcations

We can show that this complicated system is still one-dimensional (at least in space) and then we can see the effects of parameters like \(m/M\).

---

Exercise 4, baby bifurcations

4a. In terms of the rotation angle \(\phi\) of the wheel, write down the total potential energy \(U(\phi)\) of the system of both masses. Take note of any constraints that you use to write this as a 1D problem. When working this kind of problem, every object-Earth pair has gravitational potential energy and we must have the same zero of potential energy for every pair.

---

Exercise 4, baby bifurcations

4b. Use this potential energy to find values of \(m\) and \(M\) for which there are “fixed points”, “critical points”, or what we sometimes call “equilibrium points”. The language we use comes from different fields, but the concept is the same. What is the condition for the existence of any critical points?

---

Exercise 4, baby bifurcations

4c. Describe the fixed points, determine their stability, and explain why they make sense in terms of the expected motion.

---

Exercise 4, baby bifurcations

4d. Plot the potential energy for two different values of \(m/M\) and explain the differences in the potential energy graphs. Consider cases when you observe very different motion. Think about an initial condition where the mass \(m\) is at rest and the wheel is at rest. What happens when you release the mass \(m\) for your two cases?

---

Exercise 4, baby bifurcations

4e. Determine the value of \(m/M\) for which the system begins to exhibit oscillations (if released from \(\phi=0\)).

The value of \(m/M\) is a dimensionless quantity that characterizes the system and we think of it as a parameter that can change the qualitative behavior of the system.