Day 22 - Damped Oscillations

Day 22 - Damped Oscillations#

bg right width:600px

Shock absorbers are a type of damped oscillator.

They must be tuned to the weight of the car and the type of driving.

Announcements#

  • Homework 4 is graded

  • Midterm 1 is being graded

  • Homework 5 is due on Friday

  • Homework 6 is posted

  • Friday’s Class: We will discuss HW 4; Exercise 4 + Q&A

Seminars this week#

WEDNESDAY, October 15, 2025#

Astronomy Seminar, 1:30 pm, 1400 BPS, In Person and Zoom, Host ~ Adina Feinstein

Speaker: Brett Morris, Space Telescope Science Institute

Colloquium Speaker will lead a Software workshop today in this time slot.

Seminars this week#

THURSDAY, October 16, 2025#

Colloquium, 3:30 pm, 1415 BPS, in person and zoom. Host ~ Adina Feinstein

Refreshments and social half-hour in BPS 1400 starting at 3 pm

Speaker: Brett Morris, Space Telescope Science Institute Title: The Stars Behind The Planets

Zoom Link: https://msu.zoom.us/j/94951062663 Password: 2002 Or complete link: https://msu.zoom.us/j/94951062663?pwd=c48uM25P9UsRVuR74rkOioOWgpoxgC.1

Seminars this Week#

FRIDAY, October 17, 2025#

QuIC Seminar, 12:30pm, -1:30pm, 1300 BPS, In Person

Speaker: Chris Baldwin, MSU Title: TBA

Clicker Question 22-1#

My kid’s physics test was delayed until tomorrow.

How did your midterm go?

  1. It was challenging, but I was able to complete the exercises.

  2. It was difficult, and I didn’t finish all the exercises.

  3. It was interesting, I learned some new physics and modeling.

  4. It was terrible; I don’t think I was supported well to complete it.

  5. More than one of these?

Comments to share? Please do.

Reminders#

We are solving the harmonic oscillator equation: $\(\ddot{x} + \omega_0^2 x = 0\)$

We have general solutions of the form:

\[x(t) = A\cos(\omega_0 t + \delta)\]
\[x(t) = A\sin(\omega_0 t + \delta)\]
\[x(t) = A\cos(\omega_0 t) + B\sin(\omega_0 t)\]

We seek complex solutions of the form:

\[x(t) = Ae^{(i\omega_0 t + \delta)}\]

Reminders#

We denote a complex number in “Cartesian form” as:

\[z = x + iy\]

Here, \(x\) is the real part and \(y\) is the imaginary part; both are real numbers.

\[Re(z) = x \qquad Im(z) = y\]

The complex conjugate of \(z\) is:

\[z^* = \bar{z} = x - iy\]

Reminders#

We can also write a complex number in “polar form” as:

\[z = Ae^{i\delta}\]

where \(A\) is the magnitude of the complex number and \(\delta\) is the phase. Both are real numbers.

\[A = |z| = \sqrt{x^2 + y^2} \qquad \delta = \tan^{-1}\left(\frac{y}{x}\right)\]

The complex conjugate of \(z\) is: $\(z^* = \bar{z} = Ae^{-i\delta}\)$

Reminders#

The product of a complex number and its complex conjugate is:

\[z\bar{z} = (x + iy)(x - iy) = x^2 + y^2 = A^2\]

The sum of a complex number and its complex conjugate is:

\[z + \bar{z} = (x + iy) + (x - iy) = 2x = 2Re(z)\]

The difference of a complex number and its complex conjugate is:

\[z - \bar{z} = (x + iy) - (x - iy) = 2iy = 2iIm(z)\]

Clicker Question 22-1#

A complex number \(z\) is plotted in the complex plane such that \(z\) lies in the second quadrant.

bg right width:600px

Where does the complex conjugate \(z^*\) lie?

  1. In the first quadrant.

  2. In the second quadrant.

  3. In the third quadrant.

  4. In the fourth quadrant.

Visualizing the Complex Solution#

We constructed a solution of the form:

\[Ae^{i(\omega t-\delta)}\]

We can plot it in the complex plane and see the real and imaginary parts, and how they change in time.

Visualizing the Complex Solution#

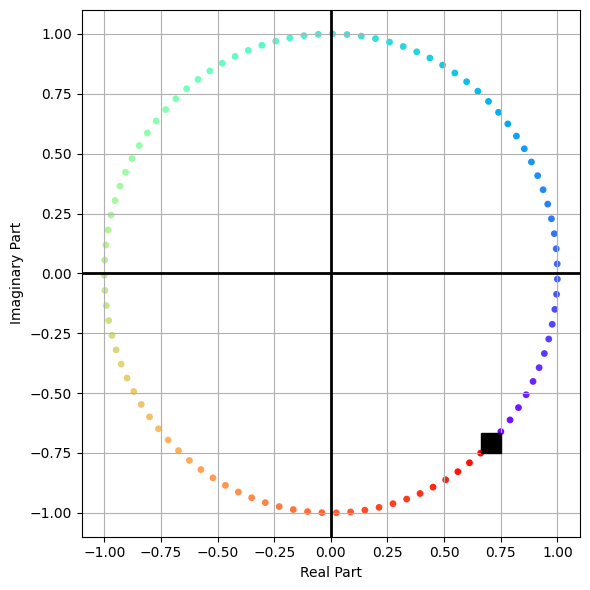
We can plot the solution on the complex plane. For this, \(\delta = \pi/4\), and the amplitude is \(A=1\).

The solution rotates counterclockwise in the complex plane, following the rainbow from violet to red.

bg right width:500px

Projecting the Real Solution#

The real part is just the projection of the complex solution onto the real axis. Just how far along the real axis is the solution at any given time.

That looks like a time trace, but not quite, it’s the real projection. The colors scheme is the same as before.

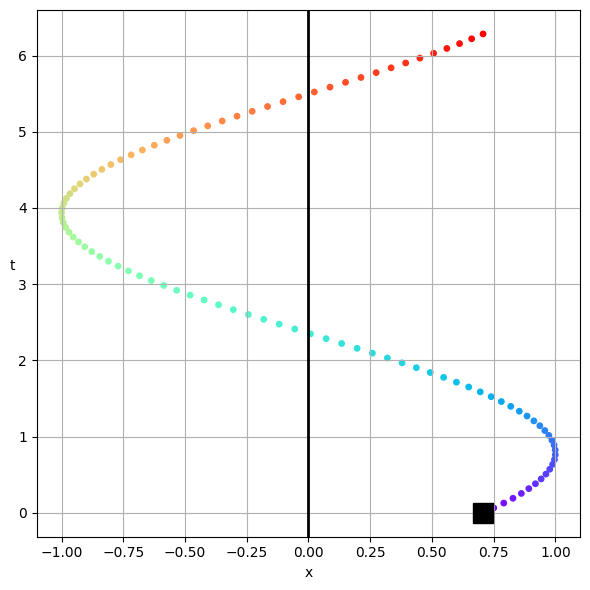
bg right width:500px

The Time Trace of the Solution#

We just flip the axes to produce the time trace that you are used to seeing. The color scheme is the same as before.

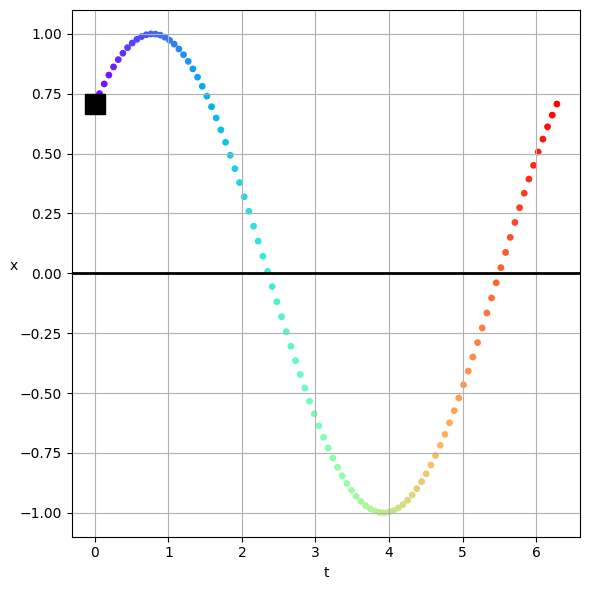
bg right width:500px

Table Activity 22-2#

We constructed a solution for the weakly damped harmonic oscillator:

\[x(t) = e^{-\beta t} \left(C_1e^{i\omega_1 t} + C_2e^{-i\omega_1 t}\right)\]

where \(\omega_1 = \sqrt{\omega_0^2 - \beta^2}\).

  • What is the physical meaning of \(\beta\)?

  • Sketch this solution, you can choose parameters, or just roughly sketch it.

  • What happens to the amplitude of the solution as time goes on?

  • Can you describe the mathematical “envelope” of the solution?

  • What is the physical meaning of this envelope?

Click when you and your table are done.

Contents