Day 19 - Phase Diagrams

Day 19 - Phase Diagrams#

Synchronization of oscillators#

right width:600px

https://www.youtube.com/watch?v=t-_VPRCtiUg

Announcements#

  • Midterm 1 is due Oct 10th (Can turn in like HW; Oct 12th at midnight)

  • Friday’s Class: Midterm 1 Help

  • Office Hours: Friday 2-4pm

    • Mihir will also be there 3-4pm to help

    • DC has to run out 30 minutes early

  • Questions over the weekend?

    • I’ll check email regularly this weekend.

    • Send me your work with your questions, please. You will get a more rapid reply with help.

Seminars this week#

WEDNESDAY, October 8, 2025#

Astronomy Seminar, 1:30 pm, 1400 BPS, In Person and Zoom, Host~ Speaker: Kyle Kremer, UC San Diego Title: Globular Clusters: Astronomical factories of gravitational-wave and electromagnetic transients Zoom Link: https://msu.zoom.us/j/94228252584?pwd=zNJdjCNAabNkppOcg5FlAv01ihzLwl.1 Meeting ID: 942 2825 2584 Passcode: 541987

Seminars this week#

THURSDAY, October 9, 2025#

Colloquium, 3:30 pm, 1415 BPS, in person and zoom. Host ~ Xing Wu Refreshments and social half-hour in BPS 1400 starting at 3 pm Speaker: Benjamin Jones, University of Texas at Arlington Title: Single Barium Ion Identification Technologies for Background-Free Neutrinoless DoubleBeta Decay searches - Zoom Link: https://msu.zoom.us/j/94951062663 Password: 2002 Or complete link: https://msu.zoom.us/j/94951062663?pwd=c48uM25P9UsRVuR74rkOioOWgpoxgC.1

Seminars this week#

FRIDAY, October 10, 2025#

QuIC Seminar, 12:30pm, -1:30pm, 1300 BPS, Zoom only Speaker: Daniel Nino, Xanadu Title: Quantum Computational Chemistry (With Pennylane) Full Scheule is at: https://sites.google.com/msu.edu/quic-seminar/ For more information, reach out to Ryan LaRose

Seminars this week#

FRIDAY, October 10, 2025#

FRIB IReNA Online Seminar, 2:00pm., Eastern Time. Hosted By: Hosted by: Borbala Cseh (Konkoly Observatory) Speaker: Artemis Spyrou, MSU Title: Neutron-capture reaction constraints for astrophysical processes Please see website for full abstract. Please click the link below to join the webinar: Join Zoom: https://msu.zoom.us/j/827950260 Meeting ID: Passcode: JINA

Reminders: Flow on a Line#

A first order ODE of the form:

\[\dot{x} = f(x)\]

can be thought of as a flow on a line. We can graph the function \(f(x)\) in the \(x\)-\(\dot{x}\) plane. Thus,

\[\dot{x} > 0 \implies f(x) > 0 \implies x \text{ is increasing}\]
\[\dot{x} < 0 \implies f(x) < 0 \implies x \text{ is decreasing}\]
\[\dot{x} = 0 \implies f(x) = 0 \implies x \text{ is a critical point}\]

So that,

\[\dot{x} > 0 \text{ means flow to the right}\]
\[\dot{x} < 0 \text{ means flow to the left}\]

Reminders: Flow on a Line#

Example \(\dot{x} = \sin{x}\)#

width:900px

Reminders: Flow on a Line#

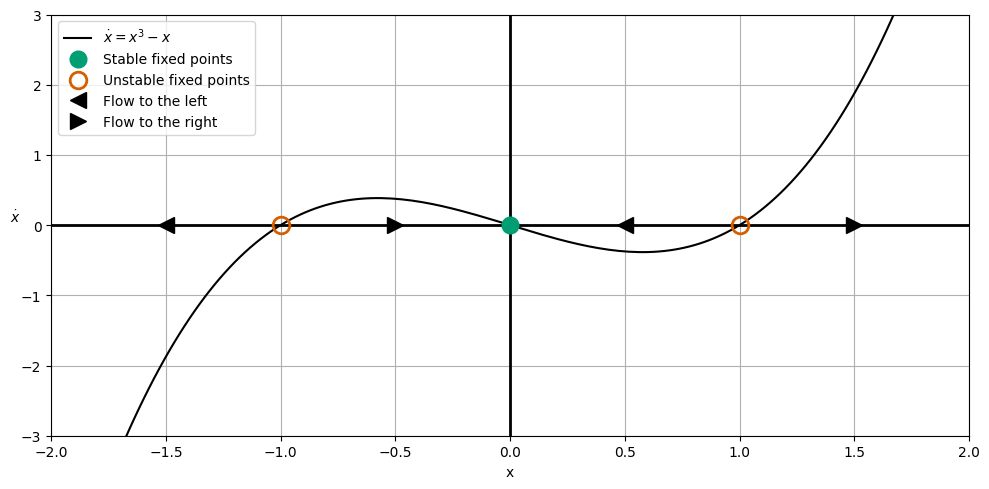
Example \(\dot{x} = x^3-x\)#

width:900px

Firefly Synchronization#

Ermentrout and Rinzel (1984) developed a model for firefly flashing.

  • The basic model suggests that a firefly will flash regularly without stimulus (\(\dot{\theta} = \omega_f\)).

  • With a flashing stimulus that flashes at its own rate (\(\dot{\Theta} = \Omega_s\)), the firefly will attempt to synchronize with the stimulus.

That model is given by

\[\dot{\phi} = \dot{\theta}-\dot{\Theta} = (\omega_f - \Omega_s) - A\sin(\Theta - \theta)\]

where the \(\phi\) is the difference in the phases (\(\theta\), firefly; \(\Theta\), stimulus) is critical to the model as is the ability of the firefly to synchronize is given by \(A\).

Firefly Synchronization#

It is typical to rescale nonlinear equations to seek natural units. In this case, we choose a dimensionless time,

\[\tau = At\]

and a dimensionless phase difference,

\[\mu = \frac{\omega_f - \Omega_s}{A}\]

Which gives the dimensionless equation for the phase difference \(\phi = \Theta - \theta\):,

\[\dfrac{d\phi}{d\tau} = \mu - \sin(\phi)\]

Clicker Question 19-1#

Consider the dimensionless equation for the phase difference \(\phi = \Theta - \theta\):

\[\dfrac{d\phi}{d\tau} = \mu - \sin(\phi)\]

Use the phase space of \(\phi\) vs. \({d\phi}/{d\tau}\) to sketch the phase diagram for the system. Find the equilibrium points and their stability. Consider the 3 cases.

  1. Assume \(\mu = 0\).

  2. Assume \(0 < \mu < 1\).

  3. Assume \(\mu > 1\).

Click when you and your table are done.#

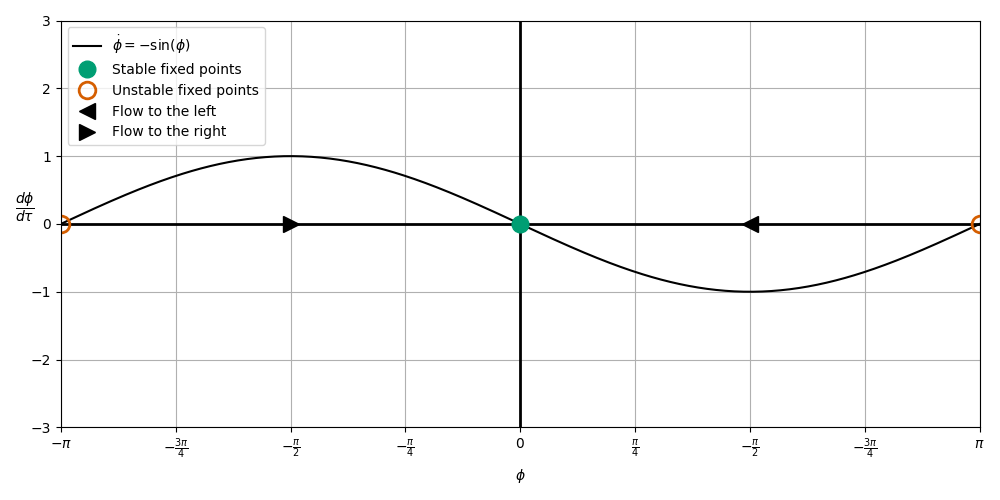
\(\mu = 0\)#

Synchronization always (no phase difference)#

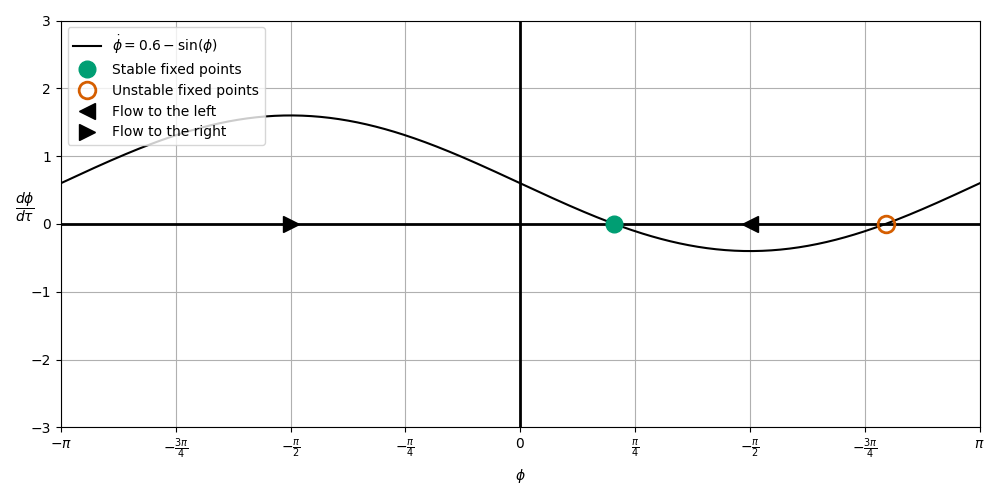
width:900px

\(\mu = 0.6\)#

Entrainment is possible (constant phase difference)#

width:900px

\(\mu=1.2\)#

No entrainment (\(\Omega > \omega\)). Stimulus is too fast.#

width:900px

Why Fireflies?#

The firefly model is a good example of a system that can be modeled with a phase diagram.

\[\dfrac{d\phi}{d\tau} = \mu - \sin(\phi)\]

  • It also has a parameter (\(\mu\)) that can be varied to change the system behavior.

  • The parameter \(\mu\) can be thought of as a “bifurcation parameter.”

  • A bifurcation is a change in the number or stability of equilibria as a parameter is varied.

  • It also illustrates the concept of “phase locking”, which is important in many spaces (e.g., lasers, Josephson junctions, etc.).

2D Phase Spaces#

What happens when we have differential equations that are not first order?

\[\ddot{x} = f(x, \dot{x})\]

We can convert this to a system of first order equations by defining a new variable \(v = \dot{x}\). Then we have a system of two first order equations:

\[\dot{x} = v\]
\[\dot{v} = f(x, v)\]

We can still use the phase space method to analyze the system in the \((x, v)\) plane.

Reminders: Phase Space and the Harmonic Oscillator#

Assume a dimensionless harmonic oscillator: $\(\ddot{x} = -x\)$

We convert this to a system of first order equations:

\[\dot{x} = v\]
\[\dot{v} = -x\]

We can graph the system in the \((x, v)\) plane.

\[\langle \dot{x}, \dot{v} \rangle = \langle v, -x \rangle\]

Steps for a Sketching a 2D Phase Diagram#

  1. Seperate the system into two first order equations.

\[\dot{x} = v\]
\[\dot{v} = -x\]

  1. At each point \((x, v)\), find the vector \(\langle \dot{x}, \dot{v} \rangle\).

  2. Represent this vector as an arrow in the \((x, v)\) plane. This gives the “flow field” of the phase space.

  3. Continue this process until you have a good representation of the flow field.

Hint: Start with points that are easy to sketch. But we will eventually use a computer to do this.

Clicker Question 19-2#

Consider the pair of first order equations:

\[\langle \dot{x}, \dot{v} \rangle = \langle v, -x \rangle\]

  1. Choose the \(x=0\) line; the vertical axis.

\[\langle \dot{x}, \dot{v} \rangle = \langle v, 0 \rangle\]

  1. Note that there will only be horizontal arrows on this line. Why?

  2. Sketch the arrows on the \(x=0\) line.

Click when you and your table are done.#

Clicker Question 19-3#

Now, SEPERATELY, please do this separately lest we draw historical symbols that we should not. Fascism has no home here, y’all.

\[\langle \dot{x}, \dot{v} \rangle = \langle v, -x \rangle\]

  1. Choose the \(v=0\) line; the vertical axis.

\[\langle \dot{x}, \dot{v} \rangle = \langle 0, -x \rangle\]

  1. Note that there will only be vertical arrows on this line. Why?

  2. Sketch the arrows on the \(v=0\) line.

Click when you and your table are done.#

Clicker Question 19-4#

Now try another line, the \(x=\pm v\) line.

\[\langle \dot{x}, \dot{v} \rangle = \langle v, \mp v \rangle\]

  1. Choose a diagonal line, \(x=v\). $\(\langle \dot{x}, \dot{v} \rangle = \langle v, -v \rangle\)$

  2. Sketch the arrows on the \(x=v\) line.

  3. Choose a diagonal line, \(x=-v\).

  4. Sketch the arrows on the \(x=-v\) line.

  5. Connect the arrows to represent the flow field as closed loops.

Click when you and your table are done.#

Flow field for the harmonic oscillator#

width:800px

Clicker Question 19-5#

bg right width:500px

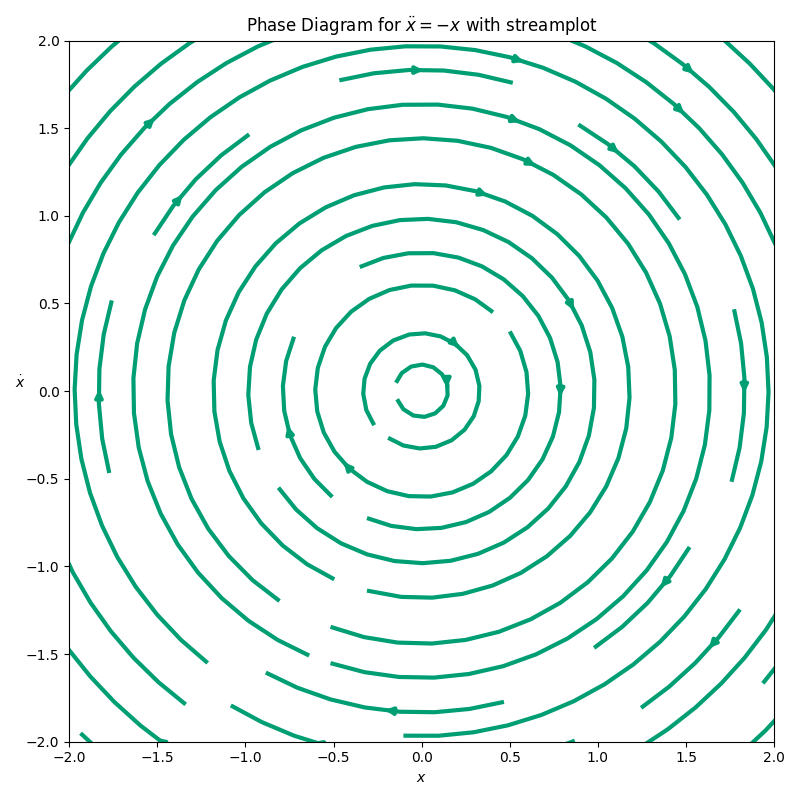
What shape are the arrows tracing out in the phase space for the harmonic oscillator?

  1. A circle

  2. An ellipse

  3. Annoying sibling voice: “A circle is an ellipse, dummy”

  4. We don’t talk like that to each other. 🥰

  5. A spiral?

Clicker Question 19-6#

bg left width:500px

These curves never touch, why is that? What does a closed curve in this phase space represent?

  1. The motion is orbital

  2. The motion is periodic.

  3. The system has constant energy.

  4. The system’s energy changes throughout.

  5. More than one of the above.

Contents