Day 09 - Modeling Drag

Day 09 - Modeling Drag#

bg right width:600px

Somersault of Paramecium in extremely confined environments ->

source: https://www.nature.com/articles/srep13148

Announcements#

  • HW 4 is posted; starting project work

  • Midterm 1 is coming up (Assigned 29 Sep; Due 10 Oct)

  • REMINDER: Office hours, for now (Mihir-MN; Danny-DC):

    • Tuesday 6-8pm (MN, Zoom)

    • Thursday 6-8pm (MN, Zoom)

    • Friday 2-4pm (DC, 1248 BPS)

  • Zoom Link: https://msu.zoom.us/j/96882248075

    • password: phy321msu

Seminars this week#

MONDAY, September 15, 2025#

Condensed Matter Seminar 4:10 pm,1400 BPS, In Person and Zoom, Host Tyler Cocker Speaker: Marcos Dantus, Michigan State University Title: Ultrafast Electron-Molecule Interactions: From Fragmentation Dynamics to H3+ Formation Zoom Link: https://msu.zoom.us/j/93613644939 Meeting ID: 936 1364 4939 Password: CMP

Seminars this week#

TUESDAY, September 16, 2025#

Theory Seminar, 11:00am., FRIB 1200 lab in person and online via Zoom Speaker: Nadezda Smirnova, CNRS Title: Isospin Symmetry Breaking and Nuclear Beta Decay Zoom Link: 964 7281 4717 Meeting ID: 48824

Seminars this week#

TUESDAY, September 16, 2025#

High Energy Physics Seminar, 1:30 pm, 1400 BPS, Host ~ Kirtimaan Mohan Speaker: Neil Christensen, Illinois State University Title: Progress in the Constructive Standard Model Zoom: Passcode: (Joining the Zoom meeting requires a password. Please contact one of the organizers, if you haven’t received it.)
Organized by: Joey Huston, Sophie Berkman and Brenda Wenzlick

Seminars this week#

WEDNESDAY, September 17, 2025#

Astronomy Seminar, 1:30 pm, 1400 BPS, In Person and Zoom, Host~ Speaker: Matthew Murphy, Michigan State University Title: Zoom Link: https://msu.zoom.us/j/887295421?pwd=N1NFb0tVU29JL2FFSkk0cStpanR3UT09 Meeting ID: 887-295-421 Passcode: 002454

Seminars this week#

WEDNESDAY, September 17, 2025#

FRIB Nuclear Science Seminar, 3:30pm., FRIB 1300 Auditorium and online via Zoom Speaker: Katie Yurkewicz of Argonne National Laboratory Title: From Nuclei to Narratives: Lessons Learned on the Journey from NSCL Student to Lab Communications Leader Please see website for full abstract. Please click the link below to join the webinar: Join Zoom: https://msu.zoom.us/j/96657965451?pwd=Isaf23sK5agzaao0Kwaei7AaWHkc4W.1 Meeting ID: 966 5796 5451 Passcode: 479842

Seminars this week#

FRIDAY, September 19, 2025#

QuIC Seminar, 12:30pm, -1:30pm, 1300 BPS, In Person
Speaker: Jeremiah Rowland, Michigan State University Title: Measurement Reduction Techniques for Measuring Hamiltonians Full Scheule is at: https://sites.google.com/msu.edu/quic-seminar/ For more information, reach out to Ryan LaRose

Reminder: email me your extra credit seminar write-ups

Goals for this week#

bg right width:600px

  • Establish a model for drag forces

  • Develop an understanding of the process for modeling forces

  • Produce equations of motion that can be investigated

  • Start probing the behavior of these systems with math and computing

Reminders#

Force Models#

We have been modeling the drag force using a functional dependence on velocity.

\[\vec{F}_{\text{drag}} = -f(v)\hat{v}\]

where \(f(v)\) is a function of velocity.

We established (in 1D) there are two common forms of drag force:

\[f(v) = bv \quad \text{Linear Drag}\]
\[f(v) = cv^2 \quad \text{Quadratic Drag}\]

Reminders#

Equations of Motion#

The next step is to use Newton’s 2nd Law to write the equations of motion for the system. We found those equation of motion to be:

\[m\dot{v} = -f(v)\]

where \(f(v)\) is the drag force. So for each form of drag we have:

\[\dot{v} = g-\frac{b}{m}v \quad \text{Linear Drag}\]
\[\dot{v} = g-\frac{c}{m}v^2 \quad \text{Quadratic Drag}\]

Reminders#

Trajectories#

We can integrate these equations of motion to find the velocity as a function of time. We found:

\[v(t) = v_{\text{t,lin}}\left(1-e^{-\frac{bt}{m}}\right) \quad \text{Linear Drag}\]
\[v(t) = v_{\text{t,quad}}\tanh\left(\frac{gt}{v_{\text{t,quad}}}\right) \quad \text{Quadratic Drag}\]

where \(v_{\text{t,lin}} = \frac{mg}{b}\) for linear drag and \(v_{\text{t,quad}} = \sqrt{\frac{mg}{c}}\) for quadratic drag.

Our Current Investigatory Process#

The Model-to-Trajectory Pipeline#

  1. Model the forces acting on the system

  2. Write the equations of motion using Newton’s 2nd Law

  3. Solve the equations of motion to find trajectories

This is incomplete. We will need to learn how stability, critical points, and phase space can help us understand the behavior of these systems.

We have also only done step 3 analytically. We will need to learn how to use computing to investigate these systems.

Clicker Question 9-1#

For the system of Linear Drag in 1D, we found a solution for the velocity as a function of time, with \(v = 0\) at \(t = 0\). $\(v(t) = v_{term}\left(1-e^{-\dfrac{bt}{m}}\right)\)$

where \(v_{term} = \sqrt{\frac{mg}{b}}\).

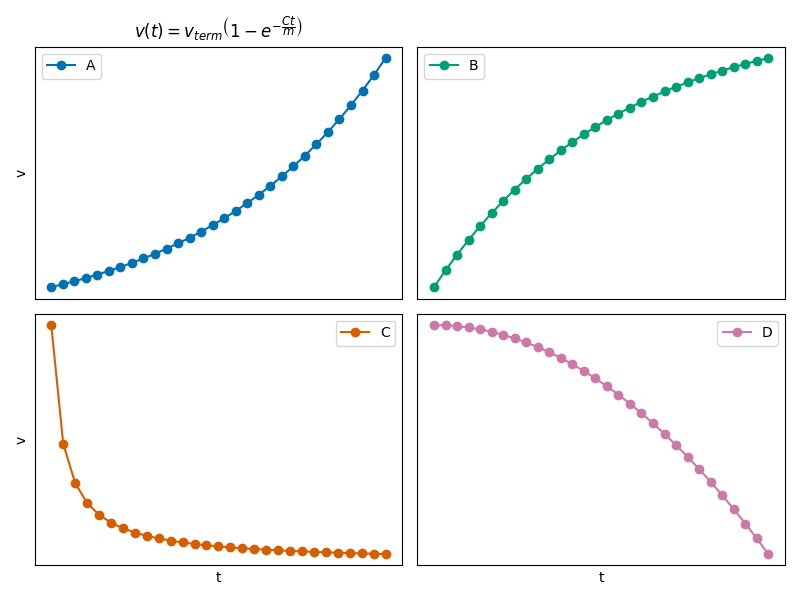
bg right w:100%

CQ 9-1#

Which sketch could be correct for the velocity of the ball?

Clicker Question 9-2#

For the system of Quadratic Drag in 1D, we found a solution for the velocity as a function of time, with \(v = 0\) at \(t = 0\).

\[v(t) = v_{term}\tanh(gt/v_{term})\]

where \(v_{term} = \sqrt{mg/c}\). What happens when \(t \rightarrow \infty\)?

  1. The object stops moving.

  2. The object travels at a constant velocity.

  3. The object travels at an increasing velocity.

  4. The object travels at a decreasing velocity.

  5. I’m not sure.

Clicker Question 9-3#

For quadratic drag in 2D, we found the following pair of differential equations:

\[\dot{v}_x = -\tilde{D}v_x\sqrt{v_x^2+v_y^2}\]
\[\dot{v}_y = -\tilde{D}v_y\sqrt{v_x^2+v_y^2}-g\]

True or False: This pair of differential equations can be decoupled.

  1. True

  2. False

  3. ???

Clicker Question 9-4#

For linear drag in 2D, we found the following pair of differential equations:

\[\dot{v}_x = -\gamma v_x\]
\[\dot{v}_y = -\gamma v_y-g\]

True or False: This pair of differential equations is decoupled.

  1. True

  2. False

  3. ???

Clicker Question 9-5#

For the gravitational interaction, I want to compute the force acting on body B, located at \(\vec{r}_B\), by body A, located at \(\vec{r}_A\).

The gravitational force is given by:

\[\vec{F} = -G\dfrac{m_1 m_2}{r^2}\hat{r}\]

What is the appropriate form of \(\vec{r}\)?

  1. \(\vec{r} = \vec{r}_A - \vec{r}_B\)

  2. \(\vec{r} = \vec{r}_B - \vec{r}_A\)

  3. Either is ok

Clicker Question 9-6#

We found that the equation of motion for the spring-mass system was:

\[\ddot{x} = -\dfrac{k}{m}x = -\omega^2 x\]

Your friends have proposed the following general solutions:

\[1.\;x(t) = A\cos(\omega t) \qquad 2.\;x(t) = B\sin(\omega t) \qquad 3.\;x(t) = A\cos(\omega t) + B\sin(\omega t) \]
\[ 4.\;x(t) = A\cos(\omega t + \phi) \qquad 5.\;x(t) = B\sin(\omega t + \phi) \qquad 6.\;x(t) = A\cos(\omega t + \phi) + B\sin(\omega t + \phi) \]

How many of them are correct? (1) Only one (2) Two (3) Three (4) Four (5) All of them

Contents