Day 06 - Making Classical Models

Day 06 - Making Classical Models#

bg right:60%

Plane Polar Coordinates Warm-Up (5 minutes)#

We introduced plane polar coordinates (\(r,\phi\)). For any position vector, \(\vec{R}\), we can write:

\[\vec{R} = \left|\vec{R}\right|\hat{r} = r\hat{r}\]

where \(r\) is the magnitude of \(\vec{R}\), and \(\hat{r}\) is the radial unit vector.

Find \(\dot{\vec{R}} = \frac{d\vec{R}}{dt}\). Get as far as you can. Our answer will be in terms of \(\hat{r}\) and \(\hat{\phi}\).

Remember the chain rule and Cartesian unit vectors are fixed in space/time

\(\hat{r} = \cos(\phi)\hat{x} + \sin(\phi)\hat{y} \qquad \hat{\phi} = -\sin(\phi)\hat{x} + \cos(\phi)\hat{y}\) \(\frac{d}{d\phi} \cos \phi = -\sin \phi \qquad \frac{d}{d\phi} \sin \phi = \cos \phi\)

Announcements#

  • Homework 2 is due Friday

  • Homework 3 is now posted

  • Office hours, for now (Mihir-MN; Danny-DC):

    • Tuesday 6-8pm (MN, Zoom)

    • Thursday 6-8pm (MN, Zoom)

    • Friday 2-4pm (DC, 1248 BPS)

  • Zoom Link: https://msu.zoom.us/j/96882248075

    • password: phy321msu

Seminars this week#

TUESDAY, September 9, 2025#

High Energy Physics Seminar, 1:30 pm, 1400 BPS, Host ~ Joey Huston Speaker: Joshua Isaacson, MSU Title: Single pion-production and pion propagation in Achilles
Organized by: Joey Huston, Sophie Berkman and Brenda Wenzlick

Seminars this week#

WEDNESDAY, September 10, 2025#

Astronomy Seminar, 1:30 pm, 1400 BPS, In Person and Zoom, Host~ Speaker: Rachael Roettenbacher, University of Michigan Title: Imaging Spotted Stars for an Improved Understanding of Stars and Exoplanets Zoom Link: https://msu.zoom.us/j/887295421?pwd=N1NFb0tVU29JL2FFSkk0cStpanR3UT09 Meeting ID: 887-295-421 Passcode: 002454

Seminars this week#

WEDNESDAY, September 10, 2025#

FRIB Nuclear Science Seminar, 3:30pm., FRIB 1300 Auditorium and online via Zoom Speaker: Suzanne Lapi of the University of Alabama at Birmingham Title: Development of new isotopes for theranostic applications Please see website for full abstract. Please click the link below to join the webinar: Join Zoom: https://msu.zoom.us/j/96485010083?pwd=O0rXwspn80aYGEI06QEZag6Ao4siq7.1 Meeting ID: 964 8501 0083 Passcode: 261744

Seminars this week#

THURSDAY, September 11, 2025#

Colloquium, 3:30 pm, 1415 BPS, in person and zoom. Host ~ Refreshments and social half-hour in BPS 1400 starting at 3 pm Speaker: Laura Chomiuk, MSU Title: Fall 2025 Physics and Astronomy Kickoff Background: For more information and to schedule time with the speaker, see the colloquium calendar at https://pa.msu.edu/news-events-seminars/colloquium-schedule.aspx Zoom Link: https://msu.zoom.us/j/94951062663 Password: 2002 Or complete link: https://msu.zoom.us/j/94951062663?pwd=c48uM25P9UsRVuR74rkOioOWgpoxgC.1

Seminars this week#

FRIDAY, September 12, 2025#

QuIC Seminar, 12:30pm, -1:30pm, 1300 BPS, In Person
Speaker: Jean Paul Sadia, MSU Title: Introduction to Quantum Information and Computation Full Scheule is at: https://sites.google.com/msu.edu/quic-seminar/ For more information, reach out to Ryan LaRose

Seminars this week#

FRIDAY, September 12, 2025#

IReNA Online Seminar, 2:00 pm, via Zoom. Hosted by: Artemis Tsantiri (University of Regina, Canada) Speaker: Lorenzo Roberti, INFN-LNS, Italy/Konkoly, Observatory Hungary Title: Carbon-Oxygen Shell Mergers in Massive Stars Zoom Link: https://msu.zoom.us/j/827950260 Password: JINA

AI Policy Proposals#

  • Proposal 1: We adopt a policy that does not allow AI use at all.

  • Proposal 2: We adopt a policy that allows AI use for brainstorming, help, and editing.

  • Proposal 3: We adopt a policy that allows AI for use in nearly any way.

  • Proposal 4: We adopt a policy that allows AI for use in any way with no documentation required.

Updated AI Policy#

We have only 12 votes! Vote now, please.

https://forms.cloud.microsoft/r/0GT4umz7qY

QR Code

Goals for Week 3#

  • Be able to answer the following questions.

    • What is Mathematical Modeling?

    • What is the process for analyzing these models?

  • Be able to solve “Simple” Motion Problems with Newton’s Laws.

Modeling Video#

Modeling Video

Source: https://www.youtube.com/watch?v=dkTncoPqo5Y

What is your experience with modeling?#

Take 2-3 min to think about your prior physics classes#

  • What models have you used? What makes that a model?

  • What made a that model good or not so good?

  • What kinds of things could you do to make a better model?

Vortex Shedding#

  • At higher Reynolds numbers, flow around objects becomes unstable.

  • This instability can lead to the formation of vortices.

  • This “shedding” of vortices can lead to vibrations and noise.

bg right:60%

Model of vortex shedding behind a cylinder#

  • Controlling vortex shedding is important in many engineering applications.

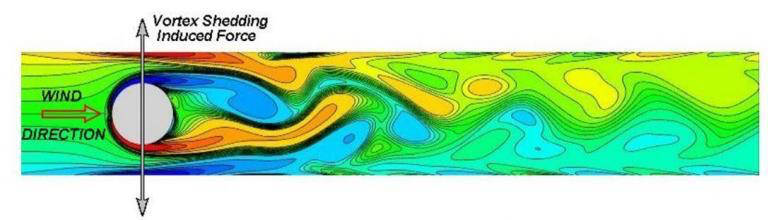
width:1000px

Giosan, Ioan, and P. Eng. "Vortex shedding induced loads on free standing structures" Structural Vortex Shedding Response Estimation Methodology and Finite Element Simulation 42 (2013).

Renewables: Wind Turbines#

Thorntonbank Wind Farm#

North Sea off the coast of Belgium#

Notice the cylindrical shape of the support structure.

bg right:40%

Clicker Question 6-1#

The SHO is a useful model: \(m\ddot{x} = -kx\).

Assume the restoring force is anti-symmetric about the equilibrium position, what is the next term model?

  1. \(\sim x^2\)

  2. \(\sim x^3\)

  3. \(\sim x^4\)

  4. \(\sim x^5\)

bg right w:80%

Clicker Question 6-2#

Assuming a linear model for Air Resistance \(\sim bv\), we obtained this EOM for a falling ball:

\[\ddot{y} = -g + \frac{b}{m}\dot{y}\]

What happens when \(\ddot{y} = 0\)?

  1. The ball stops moving (\(v = 0\)).

  2. The ball reaches a velocity of \(mg/b\).

  3. The ball reaches a terminal velocity.

  4. I’m not sure.

Clicker Question 6-3#

For the system of Linear Drag in 1D, we found a solution for the velocity as a function of time, with \(v = 0\) at \(t = 0\). $\(v(t) = v_{term}\left(1-e^{-\dfrac{bt}{m}}\right)\)$

where \(v_{term} = \sqrt{\frac{mg}{b}}\).

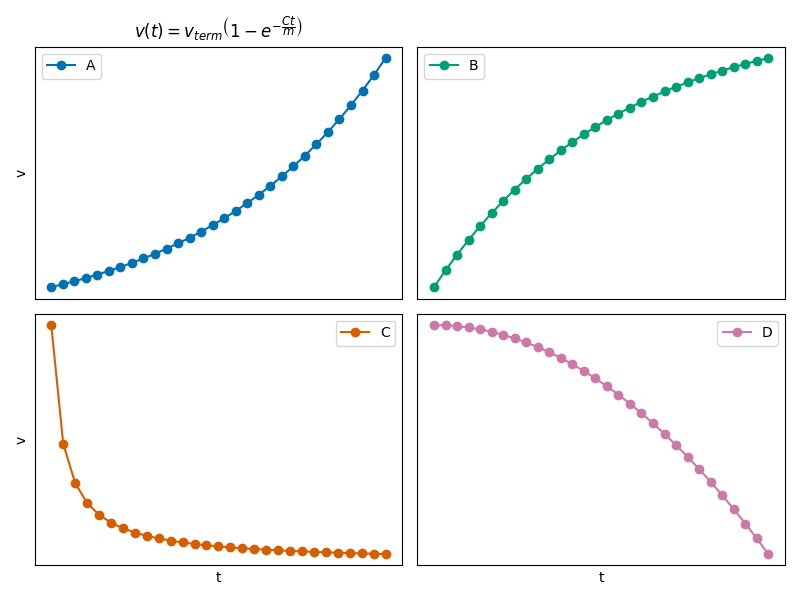
bg right w:100%

CQ 6-3#

Which sketch could be correct for the velocity of the ball?

Clicker Question 6-4#

For the system of Quadratic Drag in 1D, we found a solution for the velocity as a function of time, with \(v = 0\) at \(t = 0\).

\[v(t) = v_{term}\tanh(gt/v_{term})\]

where \(v_{term} = (mg/c)^{1/2}\). Do the units make sense? What are the units \(\left[gt/v_{term}\right]\)?

  1. Yes,\(v\) and \((mg/c)^{1/2}\) have the same units; the units for \(\left[gt/v_{term}\right]\) are m/s.

  2. No, \(v\) and \((mg/c)^{1/2}\) have different units; the units for \(\left[gt/v_{term}\right]\) are m/s.

  3. Yes, \(v\) and \((mg/c)^{1/2}\) have the same units; the units for \(\left[gt/v_{term}\right]\) are unit-less.

  4. No, \(v\) and \((mg/c)^{1/2}\) have different units; the units for \(\left[gt/v_{term}\right]\) are unit-less.

Clicker Question 6-5#

For the system of Quadratic Drag in 1D, we found a solution for the velocity as a function of time, with \(v = 0\) at \(t = 0\).

\[v(t) = v_{term}\tanh(gt/v_{term})\]

where \(v_{term} = \sqrt{mg/c}\). What happens when \(t \rightarrow \infty\)?

  1. The object stops moving.

  2. The object travels at a constant velocity.

  3. The object travels at an increasing velocity.

  4. The object travels at a decreasing velocity.

  5. I’m not sure.

Contents