Announcements

Day 02 - Newton's Laws

\[\mathbf{F}_{net} = m \mathbf{a}\]

Not shown in this picture of Newton are the countless illiterate mechanics and farmers, immigrant laborers, indigenous scholars, and other non elite members of society upon whose backs and accomplishments Newton's Principia was written.

bg right:40%

PHY 321 Classical Mechanics I - Spring 2026

Announcements#

  • Homework 1 is due next Friday (late after Sunday)

  • Help sessions will start next week

  • Friday’s class will be lead by Prof. Brian O’Shea & Mihir Naik

    • Getting started with VS Code

    • Introduce a few extensions and libraries

    • Perform numerical differentiation of a trajectory

Goals for this week#

Be able to answer the following questions:#

  • What is Classical Mechanics?

  • How can we formulate it?

  • What are the essential physics models for single particles?

  • What mathematics do we need to get started?

Think About This#

Take 2 minutes to write down what comes to mind when asked:#

What is “Classical” Physics?#

Modeling large, slow-moving objects#

Newton’s Laws are but one of a number of formulations:

  • Lagrangian Mechanics

  • Hamiltonian Mechanics

  • Dynamical Systems Theory

  • …

Key insight: Different mathematical formulations can describe the same physical phenomena, each with their own advantages for different types of problems.

An Overview of Different Physics#

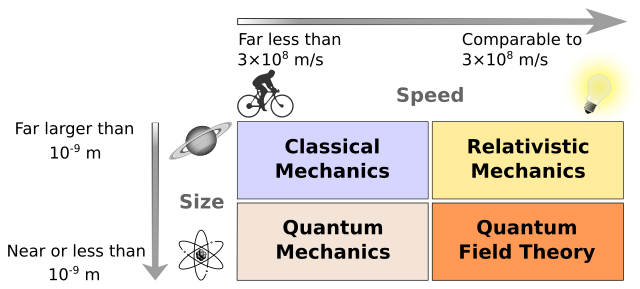
drop-shadow width:1000px

Classical Mechanics has a long history#

Wherever folks were figuring out their world, there was classical mechanics

Historical Example: Chinese Astronomy#

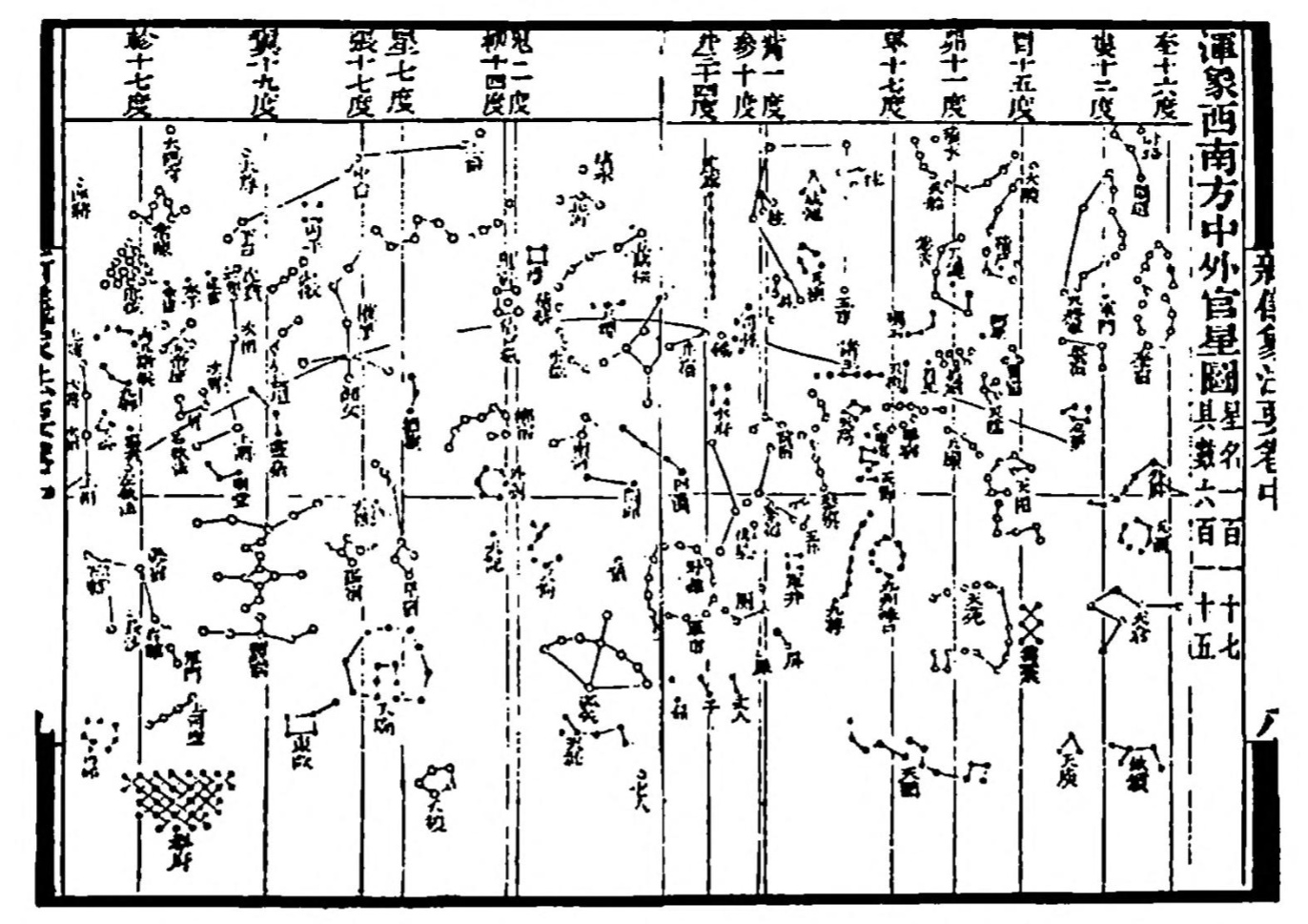
center width:600px

Song Dynasty star map showing sophisticated astronomical observations

Classical Mechanics is still very relevant#

Tiny Limbs and Long Bodies: Coordinating Lizard Locomotion
Research Lab

Tiny Limbs and Long Bodies: Coordinating Lizard Locomotion

Source: https://youtu.be/Qme07fA3Fj4

Canonical Example from Introductory Physics#

Classic problem setup:

  • Box on a ramp with a frictional interaction

  • At what angle does it slide for a given \(\mu_s\)?

bg right:45% width:500px height:auto

Canonical Example from Introductory Physics#

Key physics: Balance of forces determines the critical angle where static friction can no longer hold the box in place.

Analysis approach:

  • Decompose gravitational force into components

  • Apply Newton’s second law in each direction

  • Set acceleration to zero at the critical angle

Think-Pair-Share#

We used a tilted coordinate system (\(x-y\) plane) to analyze the motion of a block on an inclined plane. How can we check that we did the gravitational force decomposition correctly?

Recall:

  • \(F_{\text{gravity},x} = m g \sin(\theta)\)

  • \(F_{\text{gravity},y} = m g \cos(\theta)\)

Come up with at least two checks.

Clicker Question 2-1#

The formal definition of a Taylor series expansion around a point \(a\) is:

\[f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \ldots\]

This formula makes me feel:

  1. Confident, I got this.

  2. A little nervous, but I think I remember.

  3. Uncomfortable, I don’t remember this.

  4. I have no idea what this is.

Think-Pair-Share#

We derived the following differential equation for the falling ball in one-dimension:

\[\frac{d^2 y}{dt^2} = +g - \frac{b}{m} \frac{dy}{dt} - \frac{c}{m} \left(\frac{dy}{dt}\right)^2\]

Let’s assume the turbulent drag term is negligible. Is there an anti-derivative of the right-hand side of this equation? If so, what is it?

\[\frac{dv}{dt} = +g - \frac{b}{m}v\]

Example: Ball Falling in 1D in Air#

We derived the following differential equation for the motion of a ball falling in air:

\[m\ddot{y} = mg - b v - c v^2\]

We argued for low speeds, we neglect the \(v^2\) term:

\[m\ddot{y} = mg - b v\]

We can instead write this differential equation for \(v\):

\[\dot{v} = g - \frac{b}{m}v\]

Example: Ball Falling in 1D in Air#

Is this integrable? Yes!

\[\frac{dv}{dt} = g - \frac{b}{m}v\]
\[\frac{dv}{g - \frac{b}{m}v} = dt\]
\[\int \frac{dv}{g - \frac{b}{m}v} = \int dt\]

We will come back to this next week.

Vector Properties#

Newtonian Mechanics is a vector theory. Here are a few mathematical properties of vectors:

  • Addition: \(\mathbf{A} + \mathbf{B} = (A_x + B_x)\hat{x} + (A_y + B_y)\hat{y} + (A_z + B_z)\hat{z}\)

  • Scalar Multiplication: \(c\mathbf{A} = \langle cA_x, cA_y, cA_z\rangle\)

  • Dot Product: \(\mathbf{A}\cdot\mathbf{B} = A_xB_x + A_yB_y + A_zB_z = AB\cos\theta\)

  • Cross Product: \(\mathbf{A}\times\mathbf{B} = \langle A_yB_z - A_zB_y, A_zB_x - A_xB_z, A_xB_y - A_yB_x\rangle\)

  • Unit Vectors: \(\hat{A} = \frac{\mathbf{A}}{|\mathbf{A}|} \qquad |\hat{A}| = 1\)

Contents