Homework 4 (Due 13 Feb)#
Grading Breakdown
Individual Exercise (10 points) - Ex 0
Pencil and Paper Exercises (50 points) - Ex 1-5
Numerical Exercise (40 points) - Ex 6
Practicalities about homeworks
Individual exercises. You must work alone on these exercises and hand in your own answers. This should be submitted on D2L only (Homework 3 Exercise 0). Individual exercises are marked with “Individual Exercise” in the title and are counted separately from the rest of the homework.
For pencil and paper, or numerical exercises, you may work in groups of up to 3. If you work as a pair/group you may hand in one answer only if you wish. Remember to write your name(s)! These exercises are marked with “Pencil and Paper Exercises” or “Numerical Exercise” in the title, and are counted together for the homework grade.
Beyond the group you work on homework with, you may collaborate with others to discuss concepts and approaches, but you must write up your own answers (alone or as a group of 3).
Homeworks are available approximately ten days before the deadline. You should anticipate this work.
How do I(we) hand in? You can hand in the paper and pencil exercises as a single scanned PDF document. For this homework this applies to exercises 1-5. Your jupyter notebook file should be converted to a PDF file, attached to the same PDF file as for the pencil and paper exercises. All files should be uploaded to Gradescope.
Make sure your work is legible. If we cannot read it, we cannot grade it.
Individual Exercise (Submit on D2L only)#
Exercise 0 (10pt), Open Science: Reproducibility and Accessibility#
Science is a collective endeavor. Historically however, much of scientific knowledge has been represented as the work of individuals. Moreover, access to scientific knowledge has often been restricted to privileged groups through paywalls, expensive textbooks, and exclusive institutions. This has led to significant barriers for many people who wish to engage with and contribute to scientific knowledge.

Open Science is a movement that aims to make scientific research, data, and dissemination accessible to all levels of society. This includes practices such as publishing in open-access journals, sharing data and code openly, and engaging with the public through outreach and education.
Why are we reading this?
Understanding the principles and practices of Open Science is crucial for fostering a more inclusive and collaborative scientific community. By embracing Open Science, we can help to democratize access to scientific knowledge, allowing a broader range of voices and perspectives to contribute to the advancement of science.
Additionally, Open Science practices can enhance the reproducibility and transparency of scientific research, which are essential for building trust in scientific findings.
Learning about the principles of Open Science will also prepare you to be an active participant in the scientific community, whether as a researcher, educator, or informed citizen.
For this exercise, you should read/skim the Wikipedia article on Open Science and the UNESCO Recommendation on Open Science.
If you have little time, focus on the Principles of Open Science and the Advantages and Disadvantages of Open Science on the Wikipedia page, and Section IV. Areas of Action of the UNESCO report.
In ~150 words, summarize what Open Science is and why it is important to the future of scientific research.
In ~150 words, Open Science practices can help to democratize access to scientific knowledge and foster a more inclusive scientific community. What is one way that MSU and similar large research universities implement Open Science principles to benefit both their academic communities and the public at large?
In ~150 words, reflect on how you can incorporate Open Science principles into your own work as a student and future physicist or astrophysicist. What are some specific actions you can take to promote Open Science in your academic and professional endeavors? If you have prior experience with Open Science practices, feel free to share that as well.
Any genuine and complete response will receive full credit.
Submit your answers on D2L through the assignment titled “HW4 Exercise 0”.
Pencil and Paper Exercises (Submit on Gradescope only)#
Exercise 1 (15 pts), Is this a conservative force?#
Consider a particle of mass \(m\) moving in two dimensions. The particle moves from \((0,0)\) to \((1,1)\) along three different paths, \(a\), \(b\) and \(c\) as shown in the figure below.
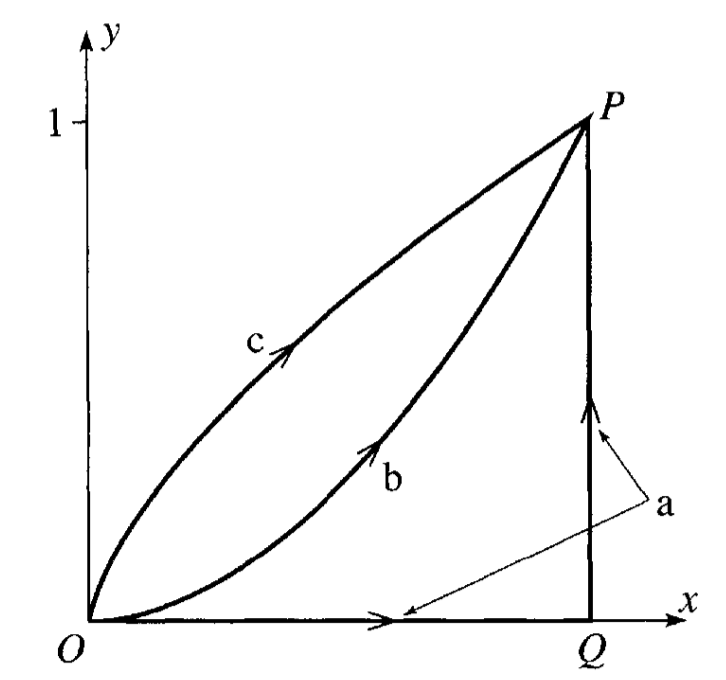
In this space, the particle experiences a force:
1a (3pt) Calculate the work done by the along path \(a\), which is a straight line from \((0,0)\) to \((1,0)\), and then to \((1,1)\). Break the path into two segments and calculate the work done along each segment separately.
1b (3pt) Calculate the work done by the force along path \(b\), which follows the function \(y = x^2\) from \((0,0)\) to \((1,1)\).
1c (4pt) Calculate the work done by the force along path \(c\), which is given parametrically by \(x = t^3\) and \(y = t^2\) from \((0,0)\) to \((1,1)\).
1d (5pt) Is this force conservative? Explain your answer in at least two ways.
Exercise 2 (10 pt), Sliding puck#
A small puck rests on a fixed sphere of radius \(R\). The puck is given a tiny nudge and it slides down the sphere. Using conservation of energy, we can determine the point at which the puck leaves the sphere.
2a (3pt) Setup the problem with a sketch. Explain the setup and include any assumptions that you need to make in order to solve the problem analytically. Identify the height as a function of the polar angle, \(h(\theta)\). What is the maximum possible angle \(\theta\) that the puck could reach before falling off? Why?
2b (2pt) Use conservation of energy to find the speed of the puck as a function of it’s height. Your answer should be in terms of the polar angle, \(\theta\).
2c (3pt) Use Newton’s Second Law to find the normal force acting on the puck as a function of it’s height. Your answer should be in terms of the polar angle, \(\theta\). What is the condition for the puck to leave the sphere?
2d (2pt) At what angle and height does the puck leave the sphere?
Exercise 3 (10pt), Example of potential#
Consider a particle of mass \(m\) moving according to the potential:
We can think of this potential as the energy landscape of a particle in three dimensions. That is, you can imagine a particle moving around this potential like a ball rolling around a landscape. That analogy is not perfect, but it is a good way to help us think about stability and equilibrium.
3a (2pt) Plot this potential or sketch a plot of it. You can use perspective plots, contour plots or any other plot you find useful.
3b (2pt) What are some feature you notice with this potential? What happens when you change \(A\) and \(a\)?
3c (2pt) Imagine a particle moving in this potential, what are some expected trajectories?
3d (2pt) Do there appear to be any equilibrium points? If so, are they stable or unstable?
3a (2pt) Is the resulting force conservative? Why?
Exercise 4 (15pt), forces and potentials#
A particle of mass \(m\) has velocity \(v=\alpha/x\), where \(x\) is its displacement.
4a (5pt) Find the force \(F(x)\) responsible for the motion.
A particle is thereafter under the influence of a force \(F=-kx+kx^3/\alpha^2\), where \(k\) and \(\alpha\) are constants and \(k\) is positive.
4b (5pt) Determine the potential \(U(x)\) and discuss the motion. It can be convenient here to make a sketch/plot of the potential as function of \(x\).
4c (5pt) What happens when the energy of the particle is \(E=(1/4)k\alpha^2\)? Hint: what is the maximum value of the potential energy?
Exercise 5 (40pt), Bouncing object#
This exercise builds on the code you wrote for solving homework 3. We recommend strongly that you study the text of Malthe-Sørenssen, section 7.5.
In homework 3 we introduced gravity and air resistance and studied their effects via a constant acceleration due to gravity and the force arising from air resistance. But what happens when the ball hits the floor? What if we would like to simulate the normal force from the floor acting on the ball? This exercise shows how we can include more complicated forces with no pain! And the force we include here is an example of a case where analytical solutions may either be difficult to find or we cannot find an analytical solution at all.
We need then to include a force model for the normal force from the floor on the ball. The simplest approach to such a system is to introduce a contact force model represented by a spring model. We model the interaction between the floor and the ball as a single spring. But the normal force is zero when there is no contact. Here we define a simple model that allows us to include such effects in our models.
The normal force from the floor on the ball is represented by a spring force. This is a strong simplification of the actual deformation process occurring at the contact between the ball and the floor due to the deformation of both the ball and the floor.
The deformed region corresponds roughly to the region of overlap between the ball and the floor. The depth of this region is \(\Delta y = R − y(t)\), where \(R\) is the radius of the ball. This is supposed to represent the compression of the spring. Our model for the normal force acting on the ball is then
The normal force must act upward when \(y < R\), hence the sign must be negative. However, we must also ensure that the normal force only acts when the ball is in contact with the floor, otherwise the normal force is zero. The full formation of the normal force is therefore
when \(y(t) < R\) and zero when \(y(t) \ge R\). In the numerical calculations you can choose \(R=0.1\) m and the spring constant \(k=1000\) N/m.
5a (10pt) Identify the forces acting on the ball and set up a diagram with the forces acting on the ball. Find the acceleration of the falling ball now with the normal force as well.
5b (10pt) Starting from the code that you write for HW3 Exercise 7 (or the posted solution), add the necessary lines of code to setup and compute these new forces (i.e., the normal interaction). What kind of control structure (e.g.,
if,try,switch) is helpful here? Write a short summary of your changes either as a comment or a separate cell. Make sure you explain the new calculations.5c (10pt) Update the code to include a plot of the ball’s height over time (i.e., \(y\) vs \(t\)). How can you tell that the plot makes sense? What should we be looking for and how do you see those features in your plot? Again, write a short summary of your changes either as a comment or a separate cell. Make sure you explain the new calculations.
5d (10pt) Using different starting (initial) conditions (i.e., \(v_0\), \(y_0\)) for the same choice of time step (\(\Delta t\)), when does your model break down? How can you tell? For reasonable values of \(v_0\) and \(y_0\) like in a physics lab, at what \(\Delta t\) does your model break down? Again, how can you tell? What do these investigations indicate is important about choosing the integration time step (\(\Delta t\)) when modeling classical systems?
Extra Credit — Integrating Research#
Earning and Submitting Your Summary
Earn up to 5 extra credit points per homework by engaging with MSU research activities. These points can boost your grade above 100% or help offset missed exercises.
Send via email to Danny caball14@msu.edu
Earn up to 5 extra credit points per homework by engaging with MSU research activities. These points can boost your grade above 100% or help offset missed exercises.
To receive full credit:
Attend an MSU research talk (see approved clubs and seminars below).
Write a summary of the talk (at least 150 words).
Submit your summary with your homework (email to caball14@msu.edu).
Approved talks include:
Society for Physics Students (SPS): Meets Monday nights (alternates with Astronomy Club)
Astronomy Club: Meets Monday nights (alternates with SPS)
Any physics and astronomy seminar of interest
Any MSU research seminar/workshop relevant to physics (get approval if unsure)
Any other physics-related event approved in advance
If you have questions, please contact Danny.
Note: You can earn 5% extra credit on each homework by attending a seminar, workshop, or other physics-related event and submitting a short reflection (about 150 words) on your experience.
