Day 27 - Hallmarks of Chaos

Day 27 - Hallmarks of Chaos#

bg right width:600px

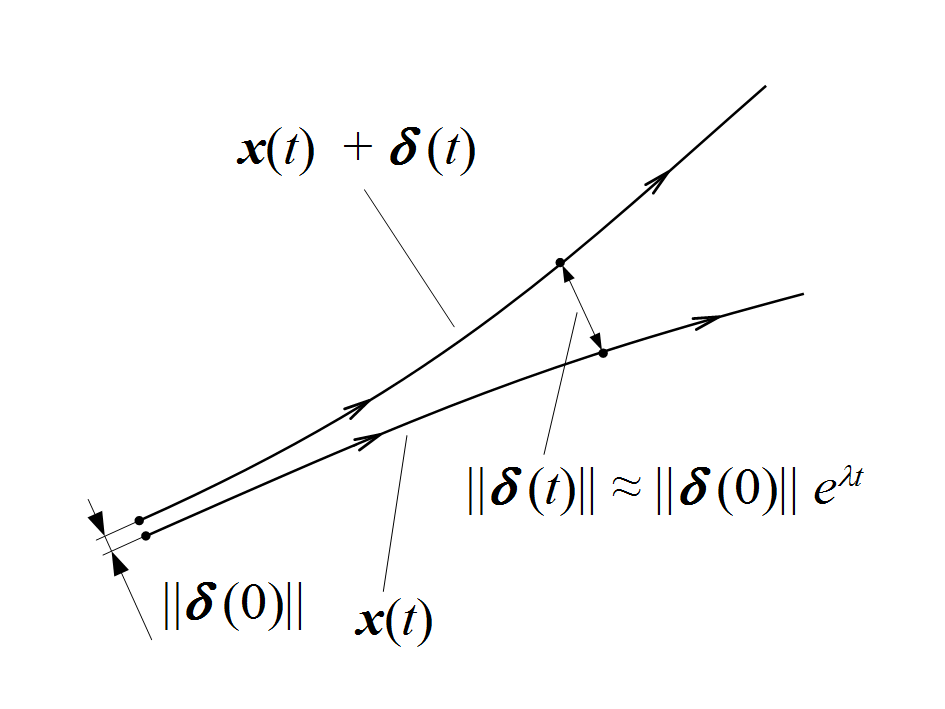
Conceptualizing the Lyapunov Exponent#

Trajectories diverge exponentially in time

Announcements#

  • Midterm 1 is graded

  • Homework 7 is due Friday

    • No homework next week

  • Midterm 2 will be assigned next Monday (due 14 November)

    • Second project check-in

  • Friday’s Class: We will work HW 7 Exercises 2 & 3 together

Seminars This Week#

WEDNESDAY, October 29, 2025#

Astronomy Seminar, 1:30 pm, 1400 BPS, In Person and Zoom, Host~ Speaker: Michael Radic, University of Chicago Title: Zoom Link: https://msu.zoom.us/j/93334479606?pwd=OtIXPWhRPBfzYu53sl3trSJlaBYI7C.1 Meeting ID: 933 3447 9606 Passcode: 825824

Seminars This Week#

WEDNESDAY, October 29, 2025#

PER (Physics Education Research Seminar), 3:00 pm., BPS 1400 in person and zoom Speaker: Eric Burkholder, Assistant Professor at Auburn University Title: Could we make physics more accessible by teaching real physics? Zoom Link: https://msu.zoom.us/j/96470703707 Meeting ID: 964 7070 3707 Passcode: PERSeminar

Seminars This Week#

WEDNESDAY, October 29, 2025#

FRIB Nuclear Science Seminar, 3:30pm., FRIB 1300 Auditorium and online via Zoom Speaker: Professor Dien Nguyen of the University of Tennessee, Knoxville Title: The Pairing Mechanism of Short Range Correlations and the impact of Nuclear Structure Please click the link below to join the webinar: Join Zoom Meeting: https://msu.zoom.us/j/93944167137?pwd=jzvwvbL8YqDnJNpzDPat8IHcrFdtC5.1 Meeting ID: 939 4416 7137 Passcode: 239049

New Course Alert: CMSE 491 – Quantum Information Science and Engineering#

Get started in the emerging field of quantum engineering!#

• 🧠 What’s it about? Quantum systems, quantum hardware, and real-world applications in computing, networking, and sensing. • 🕛 When: M/W/F 12:40–1:30 PM • 📍 Where: Farrall Agricultural Engineering Hall 119 • 👩‍🏫 Instructor: Dr. Sarah Frechette (ERC C107, rober964@msu.edu)

📘 Who’s it for?#

Physics, engineering, and computing majors—or anyone curious about quantum tech.

bg 90%

Hallmarks of a Classically Chaotic System#

  1. Deterministic

  2. Sensitive to Initial Conditions

  3. Non-periodic Behavior

  4. Strange Attractors

  5. Parameter Sensitivity

  6. (Sometimes) Periodic Behavior

Limit Cycle#

A limit cycle is a closed trajectory in phase space that is an attractor for a dynamical system.

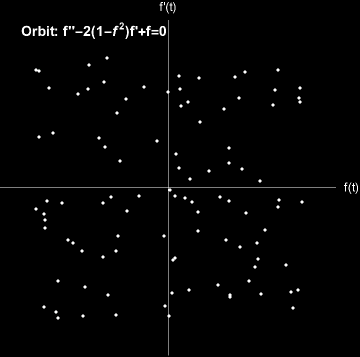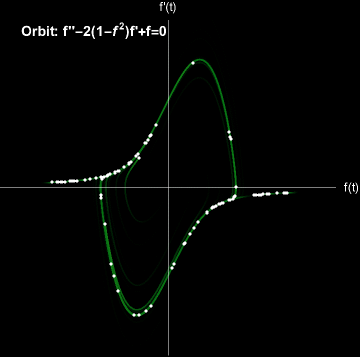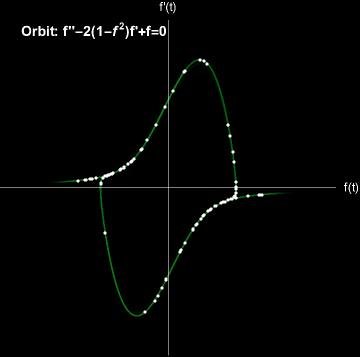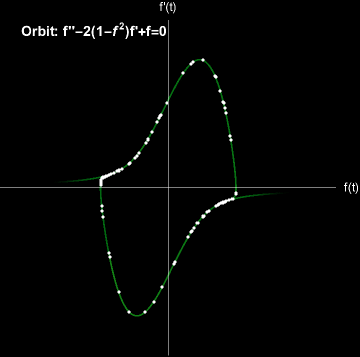
bg right

The Van der Pol Oscillator exhibits a limit cycle.

\[\ddot{x} - \mu (1 - x^2) \dot{x} + x = 0\]

Random initial conditions converge to a limit cycle. Modeled with \(\mu=2\).

The Lyapunov Exponent#

bg right width:700px

\(\vec{\delta}(t)\) is the separation vector between two trajectories in phase space \(\vec{\delta}(t) = \vec{x}_2(t) - \vec{x}_1(t)\).

Do trajectories diverge exponentially in time, \(|\vec{\delta}(t)| \approx |\vec{\delta}(0)| e^{\lambda t}\)?

Each phase coordinate can change at a different rate: \(\vec{\lambda} = \langle \lambda_1, \lambda_2, \dots, \lambda_n \rangle\).

Largest \(\lambda_i > 0\)? Chaotic system.

Strange Attractors#

A strange attractor is a set of points in phase space that a chaotic system approaches.

Chen Attractor

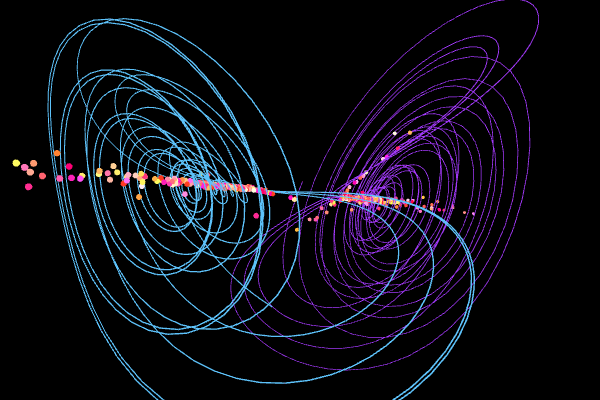
Chen Attractor bg left

\[\dot{x} = \alpha x-yz\]
\[\dot{y} = \beta y + xz\]
\[\dot{z} = \gamma z + xy/3\]

\(\alpha=5\), \(\beta=-10\), \(\gamma=-0.38\).

Interactive 3D Model

Example 1: Duffing Equation#

\[\ddot{x} + \beta \dot{x} + \alpha x + \gamma x^3 = F_0 \cos(\omega t)\]

width:1200px

Exhibits Periodic and Chaotic Behavior

Illustrates period doubling bifurcations as route to chaos

Example 2: Lorenz System#

\[\dot{x} = \sigma (y - x)\]
\[\dot{y} = x (\rho - z) - y\]
\[\dot{z} = x y - \beta z\]

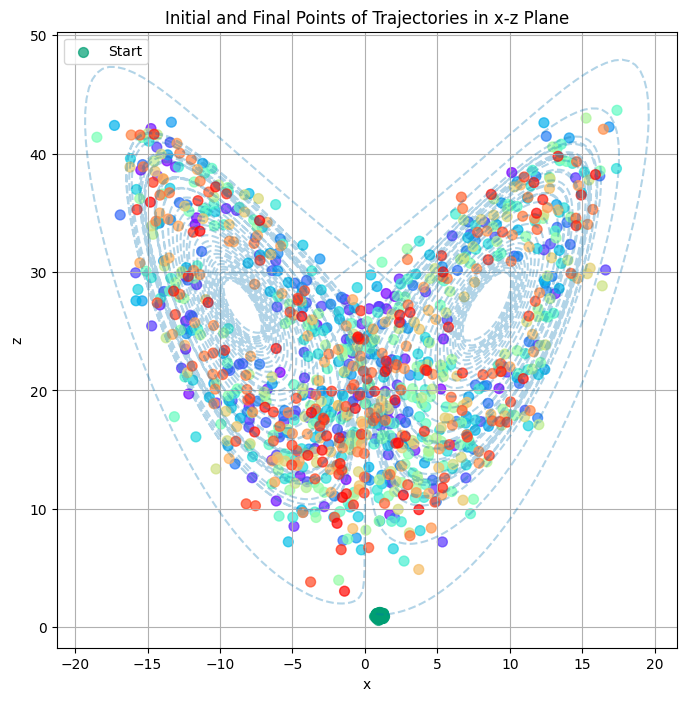
bg right width:600px

Exhibits sensitive dependence on initial conditions Demonstrates the concept of a strange attractor

Contents