Day 26 - Introduction to Chaos

Day 26 - Introduction to Chaos#

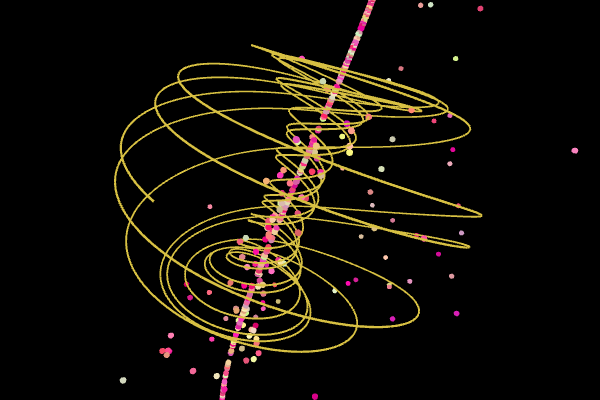
bg right width:600px

Sprott Attractor#

\[\dot{x} = y + axy +xz\]
\[\dot{y} = 1-bx^2+yz\]
\[\dot{z} = x - x^3 - y^2\]
\[a = 2.07 \quad b = 1.79\]

https://www.dynamicmath.xyz/strange-attractors/

Announcements#

  • Midterm 1 is graded

    • Feedback delivered for project

  • Homework 7 is due Friday

    • No homework next week

  • Midterm 2 will be assigned next Monday (due 14 November)

    • Second project check-in

Seminars This Week#

MONDAY, October 27, 2025#

Condensed Matter Seminar 4:10 pm,1400 BPS, In Person and Zoom, Host ~ Tyler Cocker Speaker: Elad Harel, MSU
Title: Optical Pulse Trains-From Tracking Viruses to Directing Material Synthesis Zoom Link: https://msu.zoom.us/j/93613644939 Meeting ID: 936 1364 4939 Password: CMP

Seminars This Week#

TUESDAY, October 28, 2025#

Theory Seminar, 11:00am., FRIB 1200 lab, In person and online via Zoom Speaker: Antonio Bjelcic, LLNL Title: Small and Large Amplitude Collective Dynamics within Nuclear Density Functional Theory Zoom Link: 964 7281 4717 Meeting ID: 48824

Seminars This Week#

TUESDAY, October 28, 2025#

High Energy Physics Seminar, 1:30 pm, 1400 BPS, Host~ Joey Huston Speaker: Tanishq Sharma, MSU Title: “Towards next-gen parton distribution and fragmentation functions” Zoom: Passcode: (Joining the Zoom meeting requires a password. Please contact one of the organizers, if you haven’t received it.)
Organized by: Joey Huston, Sophie Berkman and Brenda Wenzlick

Seminars This Week#

WEDNESDAY, October 29, 2025#

Astronomy Seminar, 1:30 pm, 1400 BPS, In Person and Zoom, Host~ Speaker: Michael Radic, University of Chicago Title: Zoom Link: https://msu.zoom.us/j/93334479606?pwd=OtIXPWhRPBfzYu53sl3trSJlaBYI7C.1 Meeting ID: 933 3447 9606 Passcode: 825824

Seminars This Week#

WEDNESDAY, October 29, 2025#

PER (Physics Education Research Seminar), 3:00 pm., BPS 1400 in person and zoom Speaker: Eric Burkholder, Assistant Professor at Auburn University Title: Could we make physics more accessible by teaching real physics? Zoom Link: https://msu.zoom.us/j/96470703707 Meeting ID: 964 7070 3707 Passcode: PERSeminar

Seminars This Week#

WEDNESDAY, October 29, 2025#

FRIB Nuclear Science Seminar, 3:30pm., FRIB 1300 Auditorium and online via Zoom Speaker: Professor Dien Nguyen of the University of Tennessee, Knoxville Title: The Pairing Mechanism of Short Range Correlations and the impact of Nuclear Structure Please click the link below to join the webinar: Join Zoom Meeting: https://msu.zoom.us/j/93944167137?pwd=jzvwvbL8YqDnJNpzDPat8IHcrFdtC5.1 Meeting ID: 939 4416 7137 Passcode: 239049

What is Chaos?#

bg right width:600px

At your table, discuss what it means for a system to be chaotic.

  • What are some examples of chaotic systems?

  • What are some characteristics of chaotic systems?

  • How do chaotic systems differ from non-chaotic systems?

Try to come up with two answers to each question to share.

Hallmarks of a Classically Chaotic System#

  1. Deterministic: The system is governed by deterministic laws (e.g., Newton’s laws of motion, a set of differential equations)

  2. Sensitive to Initial Conditions: A bundle of trajectories that start close together will diverge exponentially over time

  3. Non-periodic Behavior: The system exhibist s complex, non-repeating behavior over time, this might look like “random” behavior, but it is not truly random because it is deterministic

Hallmarks of a Classically Chaotic System#

  1. Strange Attractors: The system may have a strange attractor, which is a fractal structure in phase space that the system tends to evolve towards over time

  2. Parameter Sensitivity: The system may be sensitive to small changes in parameters, which can trigger qualitative changes in the system’s behavior

  3. (Sometimes) Periodic Behavior: The system may exhibit periodic behavior for certain parameter values, and this might be a signal that the system bifurcates into chaotic behavior for other parameter values

Example 1: Duffing Equation#

\[\ddot{x} + \beta \dot{x} + \alpha x + \gamma x^3 = F_0 \cos(\omega t)\]

width:1200px

Exhibits Periodic and Chaotic Behavior

Illustrates period doubling bifurcations as route to chaos

Example 2: Lorenz System#

\[\dot{x} = \sigma (y - x)\]
\[\dot{y} = x (\rho - z) - y\]
\[\dot{z} = x y - \beta z\]

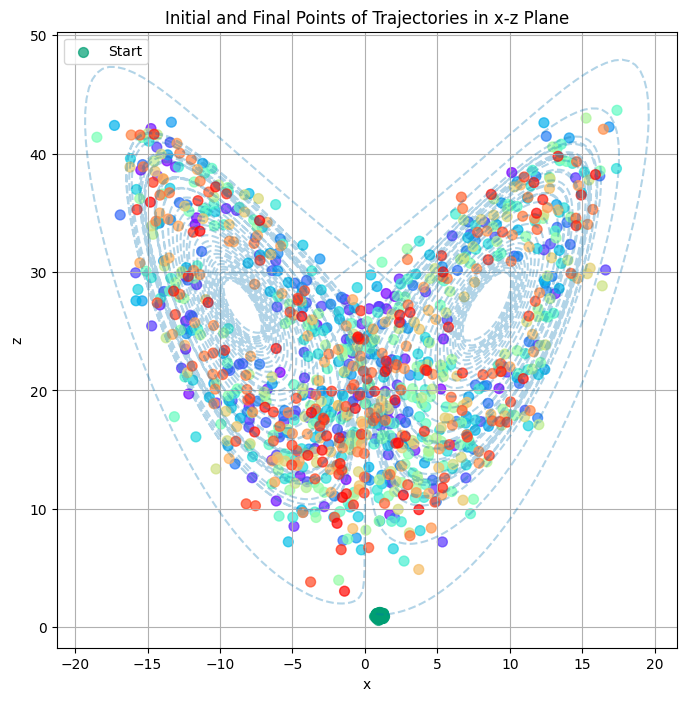
bg right width:600px

Exhibits sensitive dependence on initial conditions Demonstrates the concept of a strange attractor

Using solve_ivp#

We will start with the damped driven pendulum as an example. This will illustrate how to use solve_ivp to solve a system of coupled first-order differential equations.

\[\ddot{\theta} + \beta \dot{\theta} + \sin(\theta) = A \cos(\omega_D t)\]

We can rewrite this as two first-order equations:

\[\dot{\theta} = \omega\]
\[\dot{\omega} = -\beta \omega - \sin(\theta) + A \cos(\omega_D t)\]

Using solve_ivp#

To use solve_ivp, we write a function for the derivatives:

def damped_driven_pendulum(t, y, beta, A, omegaD=1):
    theta, omega = y
    dtheta_dt = omega
    domega_dt = -np.sin(theta) - beta * omega + A * np.cos(omegaD*t)
    return [dtheta_dt, domega_dt]

Using solve_ivp#

Now we can use solve_ivp to solve the system of equations:

# Parameters that define the system
beta = 0.5
A = 1.0
omegaD = 2*np.pi

# Time span for the simulation
t_span = (0, 100)

# Initial conditions: [theta, omega]
y0 = [6, 0]

# Time points where we want the solution
t_eval = np.linspace(t_span[0], t_span[1], 10000)

# Solve the system of equations
solution = solve_ivp(damped_driven_pendulum, t_span, y0, args=(beta, A, omegaD), t_eval=t_eval)

Damped Driven Pendulum#

Long Term Behavior is Periodic

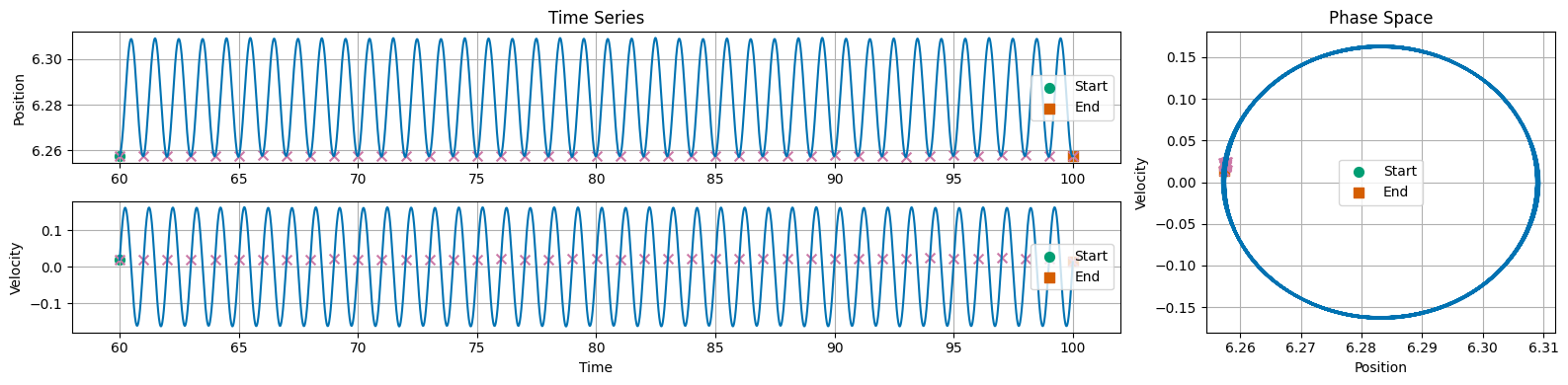
damped

“Period-1” Dynamics is a term to indicate there’s a single frequency governing the motion

Phase space plots can provide a better window into the system’s behavior

Contents