Day 04 - Mathematical Preliminaries

Questions? Make sure to upvote questions

PHY 321 Classical Mechanics I - Spring 2026

---

RaiseMyHand

• Tool should be available for each class period.

• Answers to your questions are also written up after class

  • Day 02 - https://raisemyhand.msucerl.org/student?code=s97Hf7-WS9K7b7ooovdjKxXwih1b_Nnj

• Links to each day posted in MS Teams

Would appreciate your feedback and/or ideas for use cases

---

Announcements

• Homework 1 is due this Friday

• Homework 2 is posted now

• Help sessions start this week

  • DC Friday at 2-4pm (1248 BPS)

• Mihir (ULA) will host additional help hours soon

---

Seminars this week

WEDNESDAY, January 21, 2026

Astronomy Seminar, 1:30 p.m., BPS 1400 & Zoom Speaker: Yuan Li, UMass - Amherst Title: TBA Zoom Link: https://msu.zoom.us/j/93334479606?pwd=OtIXPWhRPBfzYu53sl3trSJlaBYI7C.1 Passcode: 825824

---

Seminars this week

THURSDAY, January 22, 2026

Colloquium, Seminar, 3:30 p.m., BPS 1415 & Zoom Refreshments at 3:00 BPS in BPS 1400 Speaker: Richard Lenski, MSU Title: Dynamics and Repeatability of Evolution in a Long-Term Experiment with Bacteria Zoom Link: https://msu.zoom.us/j/94951062663 Password: 2002

---

Seminars this week

FRIDAY, January 23, 2026

QuIC, Seminar, 12:40 p.m., BPS 1300 & Zoom Speaker: Ben DalFavero, MSU Title: Fault tolerant quantum computing I

---

Goals for this week

Be able to answer the following questions.

• What are the essential physics models for single particles?

• How do we setup problems in classical mechanics?

• What mathematics do we need to get started?

• How do we solve the equations of motion?

---

Reminders from Day 03

• In a Newtonian world, we start from a vector description of motion

• Differential equations are mathematical models that describe the motion of particles

• We can use different methods to solve these differential equations

i-Clicker: https://join.iclicker.com/PRJO

---

Clicker Question 4-1

I feel confident in my abilities to use VS Code for my homework

1. Strongly Agree

2. Agree

3. We’ll see

4. Disagree

5. Strongly disagree

---

Projectile Motion

\[\mathbf{a} = \langle a_x, a_y \rangle\]

\[x_f = x_i + v_{x,i}t + \dfrac{1}{2}a_x t^2\]

\[y_f = y_i + v_{y,i}t + \dfrac{1}{2}a_y t^2\]

---

Clicker Question 4-2

For this fountain, what is the best guess for the acceleration (\(\mathbf{a} = ??\)) experienced by a fluid particle?
Assume \(y\) is positive upward; \(x\) is positive to the right.

1. \(a_x \neq 0, a_y = g\)

2. \(a_x = 0, a_y = g\)

3. \(a_x \neq 0, a_y = -g\)

4. \(a_x = 0, a_y = -g\)

5. Something else

---

Clicker Question 4-3

I feel comfortable with a discrete formulation of Newton’s Laws.

1. Yes, I got this.

2. I recall some ideas, but let’s check in.

3. I’m not sure.

4. I really don’t know what discrete formulation means here

5. ???

---

Clicker Question 4-4

The average velocity for a macroscopic time step \(\Delta t = t_f - t_i\) is given by:

\[\mathbf{v}_{avg} = \dfrac{\Delta \mathbf{r}}{dt}\]

where \(\Delta \mathbf{r} = \mathbf{r}_f - \mathbf{r}_i\). At what time do we estimate the average velocity occurs?

1. \(t_i\)

2. \(t_f\)

3. Sometime between \(t_f\) and \(t_i\)

4. \(\dfrac{t_f-t_i}{2}\)

---

Clicker Question 4-5

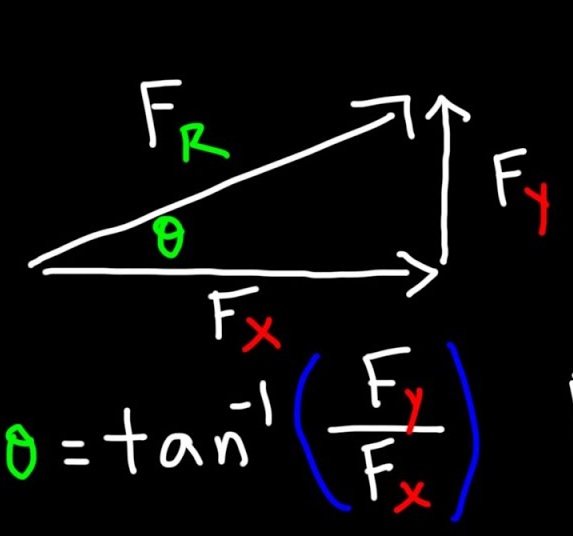
I feel comfortable with vectors, vector decomposition, and trigonometry in Cartesian coordinates.

1. Yes, I got this.

2. I recall some ideas, but let’s check in.

3. I’m not sure.

4. I don’t feel too confident with vectors.

---

Clicker Question 4-6

Consider the generic position vector \(\vec{R}\) for a particle in 2D space. Which of the following describes the direction of the vector in plane polar coordinates (\(r\), \(\phi\))?

1. \(\hat{R}\)

2. \(\hat{r}\)

3. \(\hat{\phi}\)

4. Some combination of \(\hat{r}\) and \(\hat{\phi}\)

5. I’m not sure.

---

Group Discussion 4-1

We found the following expression for the equation of motion of a falling ball subject to air resistance:

\[m \ddot{y} = +mg - b \dot{y} - c \dot{y}^2\]

What are the units of the constants \(b\) and \(c\)?

---

Group Discussion 4-2

Consider the generic position vector \(\vec{R}\) for a particle in 2D space. Find the velocity vector \(\vec{V}\) for the particle in Cartesian coordinates (\(x\), \(y\)).

What happens in plane polar coordinates?

\[\vec{R} = r \hat{r} + \phi \hat{\phi}\]

Note:

\[\hat{r} = \cos(\phi) \hat{x} + \sin(\phi) \hat{y}\]

\[\hat{\phi} = -\sin(\phi) \hat{x} + \cos(\phi) \hat{y}\]