Homework 4 (Due September 27th)

Homework 4 emphasizes another alternative method to direct integration for solving the electric field problem by reducing the vector problem to a scalar one by using electric potential. In addition, it introduces the electric potential energy concept. This homework emphasizes 2.3 and 2.4, but Sec. 2.2 (Gauss’ Law) continues to be very important.

Dropbox file request link for Homework 4

1. Overlapping clouds of charge

When solving some E&M problems, you will need to develop your argument (i.e., you solution) using an arbitrary location. In this problem, consider how choosing an arbitrary point in the overlapping region of the charge clouds will help you derive the result.

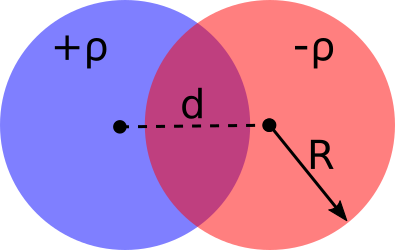
1. For a cloud of charge (radius, $R$) with uniform charge density ($\rho_0$), determine the electric field inside and outside the cloud.
2. Graph the electric field as a function of distance from the center of the cloud. Download this Jupyter notebook to create this plot (you can view it here). You will have to choose values for $\rho_0$ and $R$ to make your graph.
3. Consider two oppositely charged clouds (radii, $R$), both with uniform charge densities. They overlap like shown in the figure with their centers separated by $d$. Find the electric field in the overlapping region. (Hint: consider how Gauss’ Law and superposition can help here.)
4. In this overlapping region, sketch the electric field lines.
5. In the limit that $d$ becomes very small compared to $R$, discuss in words and make a sketch of what the resulting (total, physical) charge distribution in space really looks like (so that later in the course when we encounter such a charge distribution, we will know where it came from and what the electric field looks like inside!)

2. Using Dirac delta functions in electrostatics

Sometimes, we will describe the distribution of charge ($\rho$) using the Dirac delta function. We will need to be able to use that description to find the electric field (e.g., by using Coulomb’s Law). in this problem, you will work with the Dirac delta function to describe point charge distributions with which you are familiar. You will also find the electric field due to those charge distributions. We aim for you to gain confidence in using Dirac delta functions by checking you can find the field that you determine through other means.

1. Write down the appropriate expression for the volume charge density, $\rho(\mathbf{r})$, for a point charge, $q$, located at $\mathbf{r}’$. Interpret the units of each term in the expression.
2. Consider an electric dipole with a $+q$ charge at a location $+d$ on the $y$-axis and a $-q$ charge located at $-d$ on the $y$-axis. Write down the volume charge density, $\rho(\mathbf{r})$ for this distribution.
3. Using Coulomb’s law (direct integration), show that you can obtain the electric field of this dipole at any location $x$ on the $x$-axis.
4. Write down the appropriate expression for the volume charge distribution ($\rho$) for an infinite plane of charge at $z = a$ with surface charge density $\sigma_0$. Comment on the units of each term in your distribution.

3. Connecting potential, electric field, and charge

It is common in theoretical physics to describe the interactions of a system in terms of a scalar field (i.e., its potential). It is a compact description and you can (if you are careful) derive other important aspects of the system (e.g., how its sources are configured) from that scalar field if there is a rule for doing so. In this problem, you will do this work for a negative point charge. The understanding you draw from this problem will be used in future problems where the electric field and charge density might not be obvious.

Consider the potential of a point charge at the origin:

$$V(r) = -\dfrac{1}{4\pi\varepsilon_0}\dfrac{q}{r}$$

1. Determine the electric field of this charge by calculating the gradient ($\mathbf{E} = -\nabla V$). Show your work.
2. Calculate the charge density from the electric field by using Gauss’ Law directly ($\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$). Do this 2 ways: (1) Use the definition of the divergence from the front fly leaf of Griffiths in spherical coordinates (what do you get?) and (2) by performing a coordinate-free calculation (is your answer the same?).
3. How do your two answers from part 2 compare? Which one is correct? How do you know? What does this tell you about computing charge densities from electric potentials?

For part 2, the following vector identities might be helpful:

$$\nabla \cdot \left(f(\mathbf{r}) \mathbf{A}\right) = \nabla f(\mathbf{r}) \cdot \mathbf{A} + f(\mathbf{r}) \nabla \cdot \mathbf{A}$$ $$\nabla \cdot \dfrac{\hat{r}}{r^2} = 4\pi\delta^3(\mathbf{r})$$ $$\nabla \cdot \dfrac{\hat{r}}{r} = \dfrac{1}{r^2}$$

4. Estimating the amount of excess charge on a balloon

Developing real world estimates of certain E&M phenomenon is an important skill to develop from this course. If what we do doesn’t describe reality, what’s the point?! In this problem, you will develop an estimate for that amount of electrons transferred to a balloon through “static electricity.”

An electric field strength of 300 kV/m can cause the molecules in the air to breakdown allowing a spark to travel through the air. You have probably rubbed a ballon through your hair and heard some crackling - that is one effect of the breakdown of the molecules in the air as a result of this high field strength due to transferred electrons.

1. Estimate the minimum amount of static charge on a balloon that could cause this sparking. In your estimation, make clear any assumptions you are making and/or quantities that you are estimating or looking up. Explain how you are making this estimate in words.
2. Using your estimate in part 1, further estimate the fraction of excess electrons on the surface of the balloon compared to the number electrons that make up the balloon. Does this estimate seem reasonable to you? Why or why not?

5. Energy of a point charge distribution

When studying crystal structures (e.g., in condensed matter physics), it is sometimes convenient to model those structures as rectangular grids of charged ions, this problem offers a starting point for such a model.

Imagine a small square (side $a$) with four point charges $+q$, one on each corner.

1. Calculate the total stored energy of this system (i.e. the amount of work required to assemble it).
2. Calculate how much work it takes to “neutralize” these charges by bringing in one more point charge ($-4q$) from far away and placing it right at the center of this square.

6. Finding voltage from a charge distribution

We have found a number of ways of relating $\rho$, $\mathbf{E}$, and $V$. In this problem, you will use $\rho$ to find $V$ through the method of direct integration (i.e., using the integral expression for $V$).

1. Find a formula for the electrostatic potential $V(z)$ everywhere along the symmetry-axis of a charged ring (radius $a$, centered on the $z$-axis, with uniform linear charge density $\lambda$ around the ring). Please use the method of direct integration to do this, and set your reference point to be $V(\infty)=0$.
2. Sketch $V(z)$, how does $V(z)$ behave as $z \rightarrow \infty$? (Don’t just say it goes to zero. How does it go to zero?) Does your answer make physical sense to you? Explain briefly.
3. Use your result from part 1 for $V(0,0,z)$ to find $z$-component of the electric field anywhere along the $z$-axis?
4. What is the voltage at the origin? What is the electric field at the origin? Do these results from $V$ and $\mathbf{E}$ at the origin make physical sense to you, and are they consistent with each other? Briefly explain.