Day 15 - Potential Energy and Stability

Day 15 - Potential Energy and Stability#

bg right width:600px

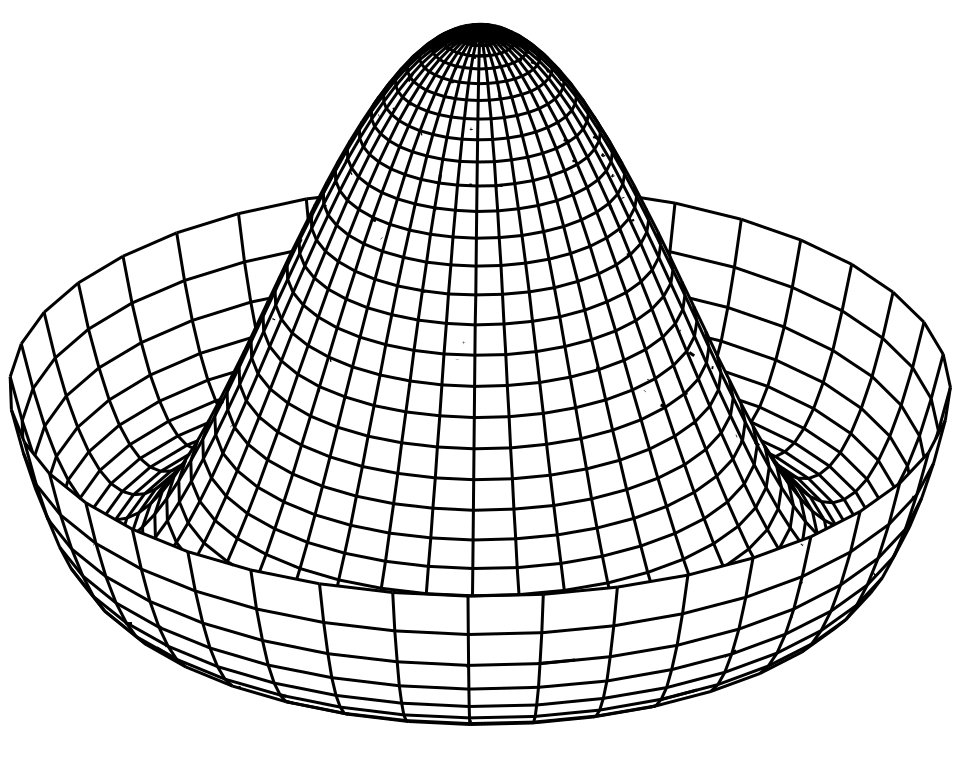
Mexican Hat/Sombrero Potential \(\longrightarrow\)

Mexican Hat Potential#

\(V(\phi) = -5|\phi|^2 + |\phi|^4\)

bg right width:80%

Announcements#

  • Midterm 1 is available today (Due Oct 10th)

  • You may work in larger groups, but solutions are submitted like homework

  • No office hours on Friday (DC traveling)

Seminars this week#

MONDAY, September 29, 2025#

Condensed Matter Seminar 4:10 pm,1400 BPS, In Person and Zoom, Host ~Mark Dykman Speaker: Peter Littlewood, University of Chicago Title: Non-Reciprocal Phase Transitions Zoom Link: https://msu.zoom.us/j/93613644939 Meeting ID: 936 1364 4939 Password: CMP

Seminars this week#

TUESDAY, September 30, 2025#

Theory Seminar, 11:00am., FRIB 1200 lab in person and online via Zoom Speaker: Debora Mroczek, University of Illinois Title: Revealing new phases of matter in neutron stars Please click the link below to join the webinar: Zoom Link: 964 7281 4717 Meeting ID: 48824

Seminars this week#

TUESDAY, September 30, 2025#

High Energy Physics Seminar, 1:30 pm, 1400 BPS, Host~ Joshua Isaacson Speaker: Tony Menzo, Joint affiliation - FNAL/Univ. of Alabama Title: The journey towards differentiable hadronization models Zoom: Passcode: (Joining the Zoom meeting requires a password. Please contact one of the organizers, if you haven’t received it.)
Organized by: Joey Huston, Sophie Berkman and Brenda Wenzlick

Seminars this week#

WEDNESDAY, October 1, 2025#

Astronomy Seminar, 1:30 pm, 1400 BPS, In Person and Zoom, Host~ Speaker: Madison Brady, MSU Title: Zoom Link: https://msu.zoom.us/j/93334479606?pwd=OtIXPWhRPBfzYu53sl3trSJlaBYI7C.1 Meeting ID: 933 3447 9606 Passcode: 825824

Seminars this week#

THURSDAY, October 2, 2025#

Colloquium, 3:30 pm, 1415 BPS, in person and zoom. Host ~ Witold Nazarewics Refreshments and social half-hour in BPS 1400 starting at 3 pm Speaker: David Dean, Thomas Jefferson National Accelerator Facility Title: From the quarks to the cosmos Background: For more information and to schedule time with the speaker, see the colloquium calendar at https://pa.msu.edu/news-events-seminars/colloquium-schedule.aspx Zoom Link: https://msu.zoom.us/j/94951062663 Password: 2002

Seminars this week#

FRIDAY, October 3, 2025#

Special Seminar, 10:00am, In Person Only, FRIB 1300 Auditorium Speaker: Sudip Bhattacharyya - Tata Institute of Fundamental Research & Massachusetts Institute of Technology Title: Thermonuclear X-ray bursts: probing neutron stars and a double-photospheric-radius-expansion Sign up to meet with Dr. Bhattacharyya (enter your name and meeting location): https://docs.google.com/spreadsheets/d/1tlw765Lf8mNOeCUJp8cWfSOvQfiF4vJDOuhKKVPXH1M/edit?usp=sharing

Seminars this week#

FRIDAY, October 3, 2025#

QuIC Seminar, 12:30pm, -1:30pm, 1300 BPS, Zoom only Speaker: Balint Pato, Duke University Title: Compass codes in quantum error correction Full Scheule is at: https://sites.google.com/msu.edu/quic-seminar/ For more information, reach out to Ryan LaRose

This Week’s Goals#

  • Understand the concept of potential energy

  • Determine the equilibrium points of a system using potential energy

  • Analyze the stability of equilibrium points

  • Define and begin to apply conservation of linear and angular momentum

Reminder: The Gradient Operator \(\nabla\)#

\(\nabla\) is a vector operator. In Cartesian coordinates: $\(\nabla = \hat{x}\dfrac{\partial}{\partial x}+\hat{y}\dfrac{\partial}{\partial y}+\hat{z}\dfrac{\partial}{\partial z} = \left\langle \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right\rangle\)$

Acting on a scalar function \(f(x,y,z)\) produces a vector:

\[\nabla f(x,y,z) = \hat{x}\dfrac{\partial f}{\partial x}+\hat{y}\dfrac{\partial f}{\partial y}+\hat{z}\dfrac{\partial f}{\partial z} = \left\langle \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z} \right\rangle\]

Reminder: The Gradient Operator \(\nabla\)#

\(\nabla\) can act on vector field (function), \(\mathbf{F}(x,y,z)\) with both dot and cross products.

Divergence (Scalar Product)#

\[\nabla \cdot \mathbf{F}(x,y,z) = \left\langle \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right\rangle \cdot \langle F_x, F_y, F_z \rangle\]
\[\nabla \cdot \mathbf{F}(x,y,z) = \dfrac{\partial F_x}{\partial x} + \dfrac{\partial F_y}{\partial y} + \dfrac{\partial F_z}{\partial z}\]

How does the vector field change in the direction of the vector?

Clicker Question 15-1a#

Which of the following fields have no divergence?

A. A B. B

  1. A

  2. B

  3. Both A and B

  4. Neither A nor B

Reminder: The Gradient Operator \(\nabla\)#

\(\nabla\) can act on vector field (function), \(\mathbf{F}(x,y,z)\) with both dot and cross products.

Curl (Vector Product)#

\[\begin{split} \nabla \times \mathbf{F}(x,y,z) = \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ F_x & F_y & F_z \end{vmatrix} \end{split}\]
\[\nabla \times \mathbf{F}(x,y,z) = \left\langle \dfrac{\partial F_z}{\partial y} - \dfrac{\partial F_y}{\partial z},\ \dfrac{\partial F_x}{\partial z} - \dfrac{\partial F_z}{\partial x},\ \dfrac{\partial F_y}{\partial x} - \dfrac{\partial F_x}{\partial y} \right\rangle\]

How does the vector field change in the direction perpendicular to the vector?

Clicker Question 15-1b#

Which of the following fields have no curl?

A. A B. B

  1. A

  2. B

  3. Both A and B

  4. Neither A nor B

Clicker Question 15-1c#

Consider a vector field with zero curl: \(\nabla \times \vec{F} = 0\). Which of the following statements is true?

  1. The field is conservative

  2. \(\int \nabla \times \vec{F} \cdot d\vec{A} = 0\)

  3. \(\oint \vec{F} \cdot d\vec{r} \neq 0\)

  4. \(\vec{F}\) is the gradient of some scalar function, e.g., \(\vec{F} = - \nabla U\)

  5. Some combination of the above

Reminders: Conservative Forces#

  • Conservative forces are those with zero curl

\[\nabla \times \vec{F} = 0\]

  • The work done by a conservative force is path-independent; on a closed path, the work done is zero

\[\oint \vec{F} \cdot d\vec{r} = 0\]

  • The force can be written as the gradient of a scalar potential energy function

\[\vec{F} = - \nabla U\]

Clicker Question 15-2#

Here’s the graph of the potential energy function \(U(x)\) for a pendulum.

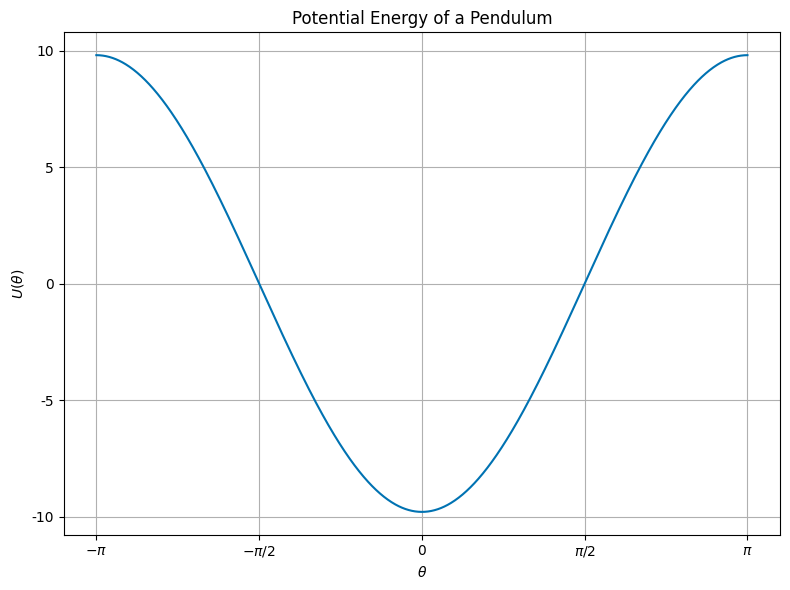
bg right width:80%

What can you say about the equilibrium points? There is/are:

  1. One stable point

  2. Two stable points

  3. One stable and one unstable point

  4. Two unstable and one stable point

Clicker Question 15-3#

Here’s a potential energy function \(U(x)\) for a pendulum:

\[U(\phi) = -mgL\cos(\phi) + U_0\]

  1. Find the equilibrium points (\(\phi^*\)) of the pendulum by setting:

\[\frac{dU(\phi^*)}{d\phi} = 0.\]

  1. Characterize the stability of the equilibrium points (\(\phi^*\)) by examining the second derivative:

\[\frac{d^2U(\phi^*)}{d\phi^2}>0? \qquad \frac{d^2U(\phi^*)}{d\phi^2}<0?\]

Click when done.

Clicker Question 15-4#

A double-well potential energy function \(U(x)\) is given by

\[U(x) = -\frac{1}{2}kx^2 + \frac{1}{4}kx^4.\]

We assume we have scaled the potential energy so that all the units are consistent.

How many equilibrium points does this system have?

  1. 1

  2. 2

  3. 3

  4. 4

Clicker Question 15-5#

A double-well potential energy function \(U(x)\) is given by

\[U(x) = -\frac{1}{2}kx^2 + \frac{1}{4}kx^4.\]

  1. Find the equilibrium points (\(x^*\)) of the pendulum by setting:

\[\frac{dU(x^*)}{dx} = 0.\]

  1. Characterize the stability of the equilibrium points (\(x^*\)) by examining the second derivative:

\[\frac{d^2U(x^*)}{dx^2}>0? \qquad \frac{d^2U(x^*)}{dx^2}<0?\]

Click when done.

Clicker Question 15-6#

Here’s a graph of the potential energy function \(U(x)\) for a double-well potential.

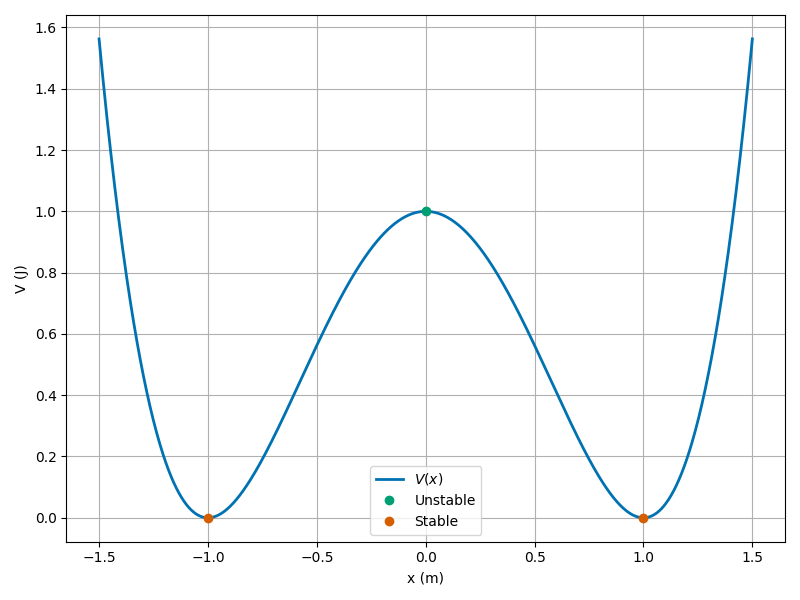
bg right width:90%

Describe the motion of a particle with the total energy, \(E=\)

  1. \(0.4\,\mathrm{J}\), \(<\) barrier height

  2. \(1.2\,\mathrm{J}\), \(>\) barrier height

  3. \(1.0\,\mathrm{J}\), \(=\) barrier height

Click when done.

Contents