Homework 7 (Due. Feb 27)

1. Slowly accumulating charge

Consider a volume current that is (very slowly) flowing towards the $z$-axis,

$$\mathbf{J} = -\dfrac{\vert c \vert s}{2} \hat{s}.$$

Charge begins to accumulate along the $z$-axis.

1. Find an expression for the accumulating charge as a function of time.
2. Determine the electric field at a distance $s$ from the $z$-axis as a function of time in all of space.
3. Determine the magnetic field in all of space due to the volume current and the accumulating charge.
4. Discuss your results in the context of conservation of energy. Which aspects of the energy are increasing/decreasing? What are you defining as the region of interest?

2. Charging Capacitor

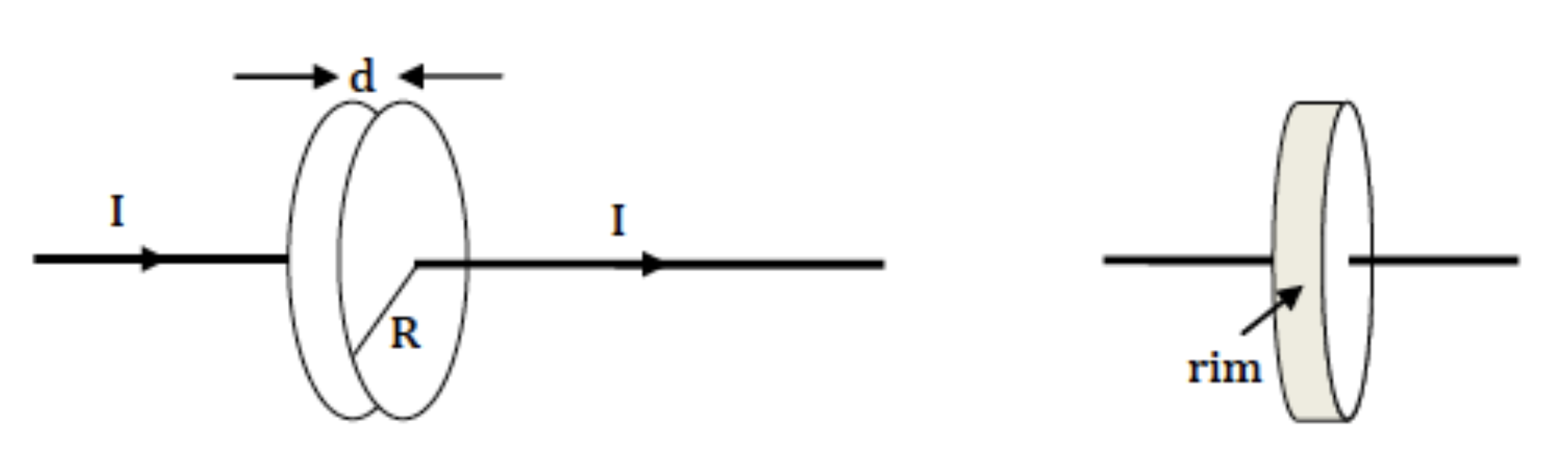
A capacitor with circular plates of radius $R$ separated by distance $d \ll R$ is being charged by a steady current $I$. The plates are sufficiently close that fringe effects can be ignored.

1. Compute the magnitude of the B-field between the plates at all distances $r$ from the center of the plates ($r < R$ & $r > R$). Sketch the magnitude of the B-field vs. $R$.
2. Compute the Poynting vector $\mathbf{S}$ (magnitude and direction) on the rim of the capacitor, between the plates, at $r = R$. (The “rim” is the ribbon of area at $r = R$ between the plates; see the diagram.)
3. Show that the rate at which the capacitor’s stored energy is increasing $dU/ dt$ is equal to the rate at which field energy is entering through the rim: $\iint \mathbf{S}\cdot d\mathbf{A}$.

3. Poynting Vector of a Solenoid

Consider a very long solenoid of length $L$, radius $r$, and turns per length $n$. The current $I$ in the solenoid is linearly ramped from $I=0$ to $I=I_0$ over a period $t_0$ as shown in the graph.

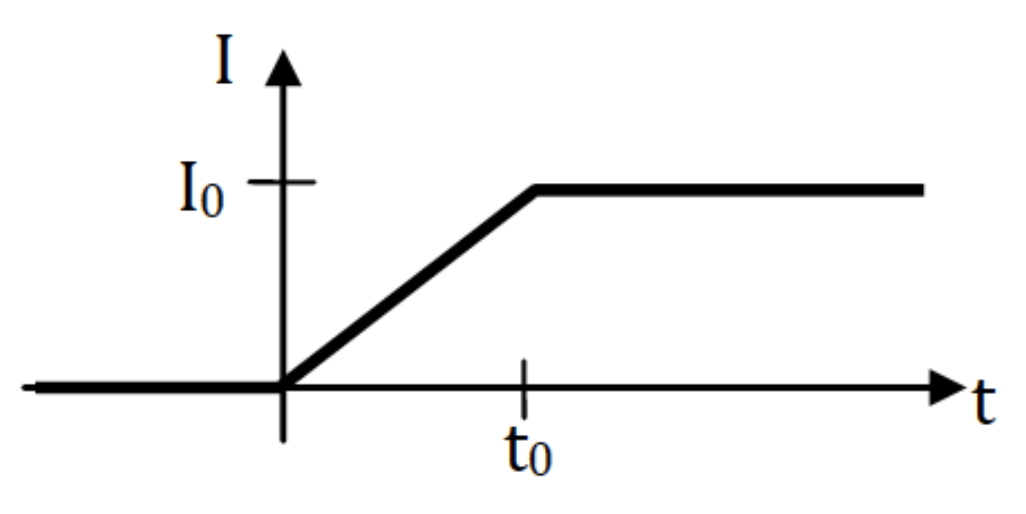
1. Integrate the magnetic field energy density to derive a formula for the total field energy stored in the solenoid at times $t > t_0$.
2. Solve for the electric field everywhere at times $0 < t < t_0$.
3. Solve for the Poynting vector $\mathbf{S}$ (direction and magnitude) at $r = R$ (just inside the walls of the solenoid) as a function of time $t$.
4. Show that the total field energy/time passing from the walls of the solenoid into its interior, when integrated from $t = 0$ to $t = t_0$, gives the same total energy as you computed in part 1.

4. Energy flow in a coax

We now want to investigate energy flow in a cylindrical coax cable. For now, let’s just look at fields constant in time, not varying in time. Assume that constant current $I$ flows in the $+z$ direction on the inner wire and that total current $I$ flows in the opposite direction in the shell. Also assume that there is a constant voltage difference $V$ between the wire and the shell, as shown.

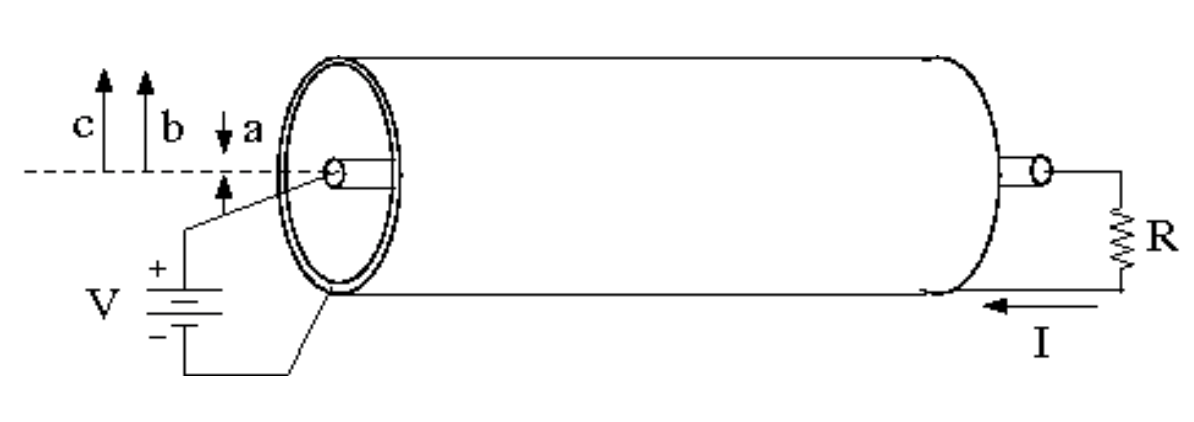
1. For this steady current and voltage case: Find $\mathbf{E}$ and $\mathbf{B}$ everywhere in space. You may assume that the coax cable (wire plus shell) is neutral.
2. Calculate the Poynting vector $\mathbf{S}$ everywhere.
3. The magnitude of $\mathbf{S}$ gives the energy flux density and represents the power per area moving through space. Does its direction make sense for the coax?
4. Integrate this flux through the cross sectional area of the coax to find the power transported down the coax line. Does your answer make sense relative to the circuit maintaining the current and voltage? Briefly comment!

5. Project Problem - Constructing an Abstract

You have completed a full draft of your paper. Now it’s time to write an abstract for this paper. An abstract summarizes your entire paper in a single paragraph. It should be self-contained and describe the entire paper in just a few sentences.

You will turn your abstract in using GitHub Classroom: HW7Q5-Abstract