Homework 3 (Due September 21st)

Link to Slack team

Homework 3 emphasizes alternative methods to direct integration (Coulomb’s Law) for solving the electric field problem including the use of Gauss’ Law and reducing the vector problem to a scalar one by using electric potential. In addition, it introduces the concept of the Dirac delta function as a tool for describing distributions of charge. This homework makes use of what you learned in Secs. 1.5, 2.2, and 2.3 (up to about 2.3.2), but what you know from 2.1 (i.e., superposition of ($\mathbf{E}$) will also be important).

Dropbox file request link for Homework 3

1. Ring of charge - Motion of a test charge

While we spend a large amount of time working with source charges and the electric fields that they produce, we are ultimately concerned about their effect on the motion of other charges (so-called “test charges”). In this problem, you will work with the electric field due to a ring of charge to develop an approximate solution for the motion of a test charge by “linearizing” the differential equation that describes the motion. In working this problem, you will have to dust off some of your classical mechanics knowledge regarding differential equations.

Consider a thin ring (positive charge, $Q$; radius, $a$) that has its central axis directed along the $x$-direction as shown.

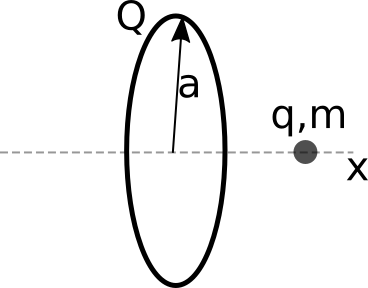
A charged ring with these parameters will produce an electric field along its central axis given by,

1. Write down the differential equation that describes the motion of a particle with negative charge $-q$ and mass $m$ that is carefully positioned on the $x$-axis. Note: this particle has a charge that is opposite the sign of the ring, so $q$ is the magnitude of the charge of this particle.
2. What kind of motion do you expect to see for this charge? Why? Does the differential equation describe that kind of motion? Hint: Consider if this differential equation is analytically tractable (i.e., can it be solved in closed form).
3. Consider the situation where the particle is very close to a large ring (i.e., where $x/a\;«\;1$). Determine the approximate form of the differential equation for this case – keep only terms that depend linearly on $x$. This is called “linearizing” the differential equation and makes the solution analytically tractable.
4. Solve the differential equation for the case where the particle starts from rest at a distance of $x_0$ from the ring. Sketch the resulting motion of the test charge as a function of time. Does your graph agree with your intuition about the motion?
5. What would happen to the test charge if it was not placed precisely on the central axis? Why?
6. We have created a Jupyter notebook that begins to model the motion of the test charge using both the exact and the approximate differential equation. You can download it here (or view it here). By working through this notebook, we expect you to complete the model and be able to explain the output of each model and its assumptions. We also ask that you determine under what conditions the approximate model is a good one and explain how you know.
7. BONUS: Break up the ring into small chunks, so that you can determine the electric field at any point. Model the motion of the charged particle in general in the presence of this charged ring. Can you get any interesting or cool trajectories? How would you plot this in 3D? This BONUS is worth 15 points (about one full problem).

2. Finding the electric field of spherical shell using direct integration

In this class, you will learn a mathematical technique (Gauss’ Law) that makes solving for the electric field relatively simple in comparison to direct integration for certain kinds of problems. In this problem, you will solve for the electric field that can be determined using Gauss’ Law, but you will use direct integration instead. This problem involves relatively sophisticated integral, which you are free to look up, have some software solve, or (for the gluttons for pain) solve yourself. The message here is: when you run across a difficult piece of math, it’s ok to use your resources; just cite your sources!

1. Find the electric field a distance $z$ above the center of a spherical shell of radius $R$, which carries a uniform surface charge density $\sigma$. Do this by explicit integration (i.e., starting from Griffith’s equation 2.7), please. Just treat the case of $z > R$ (outside the sphere). Express your answer in terms of the total charge $q$ on the sphere. Also, be careful, when you get a square root, to take the positive root: $\sqrt{R^2 + z^2 - 2Rz}=(R-z)$ if $R>z$, but it’s $(z-R)$ if $R<z$.
2. Check your answer using a units check and your knowledge from PHY 184. Briefly discuss what the answer should be outside the sphere. What should the answer be inside the sphere and why? You don’t have to solve that problem explicitly.

Historical note: Newton solved part 1 using geometry (no calculus!!) This geometric proof is tricky and still excites debate: see R. Weinstock Am. J. Phys., 52, (1984), p. 883; H. Erlichson, Am. J. Phys. 58, (1990) p. 882. Newton thought calculus should be kept secret, and held up publication of Principia until he could work out these non-calculus proofs. He published calculus much later, about the same time as Leibniz published his calculus.

3. Comparing Coulomb’s Law to Gauss’ Law

Now that we have, in principle, fully described how to solve any electrostatics problem (i.e., by adding up the contribution of each chunk of charge), we turn to building our theoretical toolbox by learning alternative methods that make the solving of certain kinds of problems more tractable. The first of these alternatives is Gauss’ Law. It is important to know when and how to apply Gauss’ Law - in the problem below, you are asked to compare Gauss’ Law with Coulomb’s Law.

Consider the following questions in finding the electric field everywhere for a conducting sphere, a uniformly charged sphere, and a sphere with charge distribution varying as $r^n$, all with radius $r_0$ and total charge $Q$:

1. What are the advantages and disadvantages of using Gauss’ Law to find the electric field instead of using Coulomb’s Law (Griffiths Eq 2.8)? What role does symmetry play?
2. Answer the same questions for three cubes with the same properties (i.e., charge distributions that vary radially as $r^n$).
3. What do your answers to parts 1 and 2 tell you about using Gauss’ Law versus using Coulomb’s Law (direct integration) to solve for the electric field?

4. Spherical charge distributions are special

As you might have picked up by now, spherically symmetric charge distributions are very special. We have a number of theoretical tools we can bring to bear on them and the results we produce are often quite simple in a mathematical sense. In this problem, you will explore these distributions a bit more and connect the mathematics (i.e., the integrals you must do) to the geometry of the problem (i.e., where the charge lives) to gain intuition about these spherically symmetric distributions of charge.

For parts 1 and 2, consider a sphere of radius $R$, centered one the origin, with a radially symmetric charge distribution $\rho(r)$.

1. What $\rho(r)$ is required for the electric field in the sphere to have the power law form $E(r) = cr^n$, where $c$ and $n$ are constants? The case of n=-2 is special. How so? Some values of $n$ are unphysical because these would lead to an infinite amount of charge in the sphere.. Which values of $n$ are allowed?
2. What kind of charge distribution is required for the radial E-field inside the sphere to be of constant magnitude; that is, what $\rho(r)$ produces $E(r) = $ constant (inside only)? Is this distribution physical realizable? Why or why not?
3. For each of these allowable charge distributions, what does the electric field look like outside the sphere ($r>R$)?
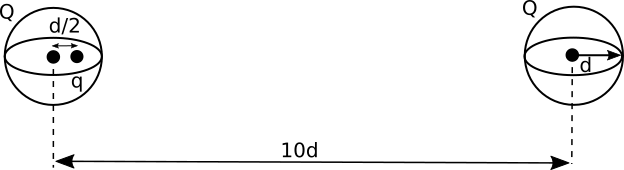
4. The following problem is from the 2001 Physics GRE Exam. Students were expected to solve the problem in just a few minutes! Two spherical, nonconducting, and very thin shells of uniformly distributed positive charge $Q$ and radius $d$ are located a distance 10$d$ apart. A positive point charge $q$ is placed inside on of the shells at a distance $d/2$ from the center, on the line connecting the centers of the two shells, as shown in the figure. What is the net force on the charge $q$?

5. Cube with a hole

What happens when you have problems were the symmetries are mixed? How do you tackle a problem with two different geometries? In this problem, you will explore how to deal with situations where they are two “competing” geometries for the problem. Sometimes you will need to bring two (or more!) aspects of your theoretical toolbox to bear on a problem.

Consider a cube (edge length $a$) with a uniform charge distributed throughout its volume ($\rho$). We carve a spherical cavity out of it of radius $d$, such that the cavity is centered at the center of the cube.

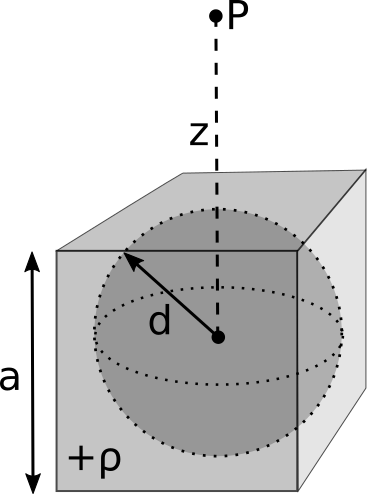
1. Does Gauss’ Law hold for this problem? Can Gauss’ Law be used on this problem? If so, what surface do you use? If not, why?
2. Let the center of the cube (and thus the center of the cavity) be located at the origin $\langle 0,0,0 \rangle$. Explain how you would determine the electric field at point $P$ a distance $z$ from the center of the cube.
3. What should your expression for the electric field be as $d$ goes to zero? What does this correspond to physically?

6. Describing charge distributions with delta functions

The Dirac delta function is an important theoretical tool for describing distributions of a variety of physical quantities (e.g., mass, charge) where a point object (or system of point objects) is the model we intend to use. In addition, it can be used to describe distributions where these quantities exist in highly constrained spaces (e.g., on a plane or spherical shell). In this class, we will use the Dirac delta function to describe how a charges are distributed. In this problem, you will get familiar with the Dirac delta function for a set point charges on a line.

The linear charge density for a series of charges on the $x$-axis is given by:

1. Write a sentence or two describing the units of each term in the equation. (Don’t forget the delta function!)
2. What is the total charge on $x$-axis?

7. A rod with a hole drilled in it

Gauss’ Law can be useful in situations where you want to determine the electric field in conceptually different physical spaces. In this problem, you will explore this using the example of a uniformly charged rod with a hole drilled through it.

Consider a rod of length $L$ and radius $b$ that has a hole drilled down the center of it (along it’s length-wise axis) with a radius of $a$. The rod is very long compared to it’s radius, so that Gauss’ Law can be used to find the approximate electric field near the middle of the rod (far from the ends). The rod has a uniform charge distribution $\rho$. You will determine the electric field “everywhere” - meaning everywhere near the middle of the rod.

1. Find the electric field inside the hole ($r<a$).
2. Find the electric field outside the rod ($r>b$).
3. Find the electric field between the hole and outer surface of the rod ($a<r<b$).
4. Why did you need to solve Gauss’ Law 3 times in this case to find the electric field “everywhere”?
5. Compare the value of the electric field right at the material boundaries ($r=a$ and $r=b$), do the values match? As we will find this matching has important implications for bound charge on material surfaces.