Homework 9 (Due 19 Apr)#

Due Apr 19 (midnight)

Date: Apr 8, 2024 Total points: 100

import numpy as np
from math import *
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
plt.style.use('seaborn-v0_8-colorblind')

Introduction to Homework 9#

This week’s exercises focus on Lagrangian Dynamics. The relevant reading background is:

  1. chapter 6.1-6.3, 7.1-7.7, 7.10 of Taylor

  2. chapter 9.1-9.5 of Boas

In both textbooks there are many nice worked out examples.

Practicalities about homeworks and projects#

  1. You can work in groups (optimal groups are often 2-3 people) or by yourself. If you work as a group you can hand in one answer only if you wish. Remember to write your name(s)!

  2. Homeworks are available ten days before the deadline.

  3. How do I (we) hand in? You can hand in the paper and pencil exercises as a scanned document. For this homework this applies to exercises 1-4. Alternatively, you can hand in everything (if you are ok with typing mathematical formulae using say Latex) as a jupyter notebook at D2L. The numerical exercise(s) (exercise 5-6 here) should always be handed in as a jupyter notebook by the deadline at D2L.

Exercise 1 (10pt) Modifying Lagrangians for friction#

We have seen that we have develop the Lagrangian formalism for a potential that depends on location \(U({q}_1, {q}_2, \dots, {q}_N)\) and a kinetic energy term that depends on speeds \(T(\dot{q}_1, \dot{q}_2, \dots, \dot{q}_N)\). But we’ve said nothing about friction.

Consider a single particle in one dimension that moves in a potential \(U(x)\) and is subject to a frictional force \(F_{fric}\).

  1. (5 pt) Write down the Lagrangian for this system.

  2. (5 pt) Show that you can write an equation of motion for this system in the form,

\[\frac{\partial L}{\partial x} + F_{fric} = \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right).\]

Exercise 2 (15pt) Modeling a Yo-yo#

Yo-yo

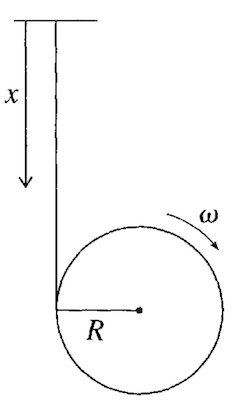
We have a rough model of a yo-yo above, really just a cylinder of mass \(m\) and radius \(R\) that can roll out on the string under the influence of gravity. The string is massless and inextensible. Choose the coordinate \(x\) as shown to be the generalized coordinate.

  1. (7 pt) Write down the Lagrangian for this system.

  2. (8 pt) Show that the cylinder accelerates at a rate \(2g/3\).

Exercise 3 (15pt) Constrained to a helix#

A bead is constrained to move on a helix with \(\rho = a\) and \(z = b\phi\), where \(a\) and \(b\) are constants. The helix is oriented upright, so the \(z\) axis is vertical. The bead is subject to a gravitational force \(-mg\hat{z}\).

  1. (5 pt) Write down the Lagrangian for this system.

  2. (5 pt) Find the equations of motion for this system. Explain what the motion of the bead looks like.

  3. (5 pt) What happens when \(a \rightarrow 0\)? Explain what the motion of the bead looks like in this limit.

Exercise 4 (25pt) Lagrangians with rotating systems#

As we develop more complicated systems, we will encounter rotating systems. In this problem, we will consider a simple example of a rotating system. A bead is constrained to move on a straight frictionless rod. The rod can pivot about it’s center (like it’s spinning on a table). The rod rotates with a constant angular velocity \(\omega\) its center.

  1. (5pt) Write down the Lagrangian for the threaded bead using \(r\) as the generalized coordinate. Note: how is \(\phi\) related to \(\omega\)?

  2. (5pt) Find the equations of motion for this system, and solve for \(r(t)\).

  3. (5pt) What happens if the bead starts at rest at \(r = r_0\)? What is the motion of the bead?

  4. (5pt) If it released from rest at \(r = r_0\), what is the motion of the bead? Explain in terms of the centrifugal force (\(m\omega^2r\)).

  5. (5pt) What have you noticed about solving this problem, which is different from the other problems we’ve done so far?

Exercise 5 (35 pt) Driven Pendulum#

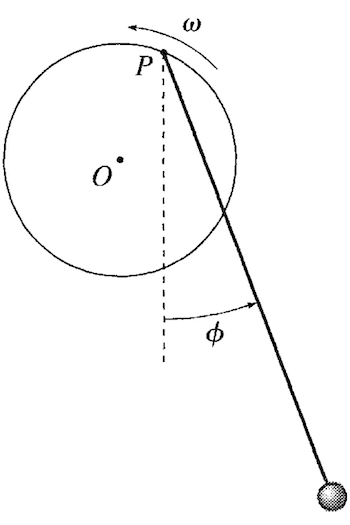
Pendulum

The pendulum above is driven by a motor that rotates the wheel shown. The set up is the wheel of radius \(R\) rotates at a constant angular velocity \(\omega\). The pendulum is free to swing in the vertical plane. The pendulum has length \(l\) and mass \(m\). The pendulum is attached the edge of the wheel at point \(P\). The wheel rotates about it’s own center \(O\).

  1. (5 pt) Write down the Lagrangian for this system.

  2. (5 pt) Find the equations of motion for \(\phi\) - be careful with \(T\), check when \(\omega =0\)

  3. (5 pt) Take the limit that the wheel rotates very slowly, and the radius of the wheel is quite small. Find the equations of motion for \(\phi\) in this limit. Describe the motion of the pendulum.

  4. (20 pt) Write (or reuse) a numerical code to solve the equations of motion for \(\phi\) for the general case. Plot the motion for at least 3 interesting cases that you find. Explain the motion of the pendulum in each case.

Extra Credit - Integrating Classwork With Research#

This opportunity will allow you to earn up to 5 extra credit points on a Homework per week. These points can push you above 100% or help make up for missed exercises. In order to earn all points you must:

  1. Attend an MSU research talk (recommended research oriented Clubs is provided below)

  2. Summarize the talk using at least 150 words

  3. Turn in the summary along with your Homework.

Approved talks: Talks given by researchers through the following clubs:

  • Research and Idea Sharing Enterprise (RAISE)​: Meets Wednesday Nights Society for Physics Students (SPS)​: Meets Monday Nights

  • Astronomy Club​: Meets Monday Nights

  • Facility For Rare Isotope Beam (FRIB) Seminars: ​Occur multiple times a week