Homework 13 (Due. Apr 20)
1. Magnetic field of a wire
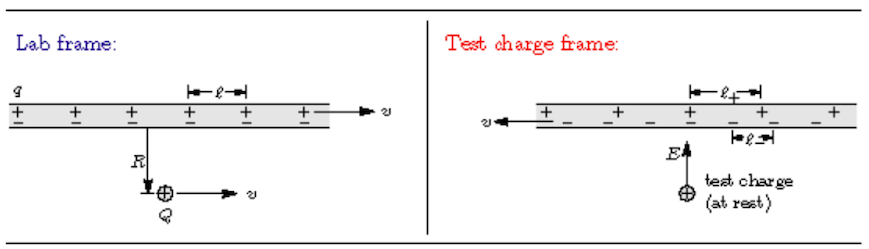
Shown above is a model of a wire with a current flowing to the right. To avoid minus signs we take the current to consist of a flow of positive charge carriers, each with charge $+q$, separated by an average distance of $l$. The wire is electrically neutral in the lab frame, so there must also be a bunch of negative charges, at rest, separated by the same average distance $l$ in this frame. Be aware that charge is Lorenz invariant: a charge Q has the same value in every inertial frame.
- Using Gauss’ law, what is the electric field outside this wire in the lab frame? Suppose there is a test charge $+Q$ outside the wire, a distance $R$ from the center of the wire, moving to the right (For simplicity, let’s say the velocity is the same as that of the moving charges in the wire, i.e. $v$, as shown in the figure.)
- Given your answer for the E-field, what is the electrostatic force on this charge, in this frame?
- Using Ampere’s (and the Lorentz force) law - what is the magnetic force on the moving test charge $Q$?
- Put it together, what is the magnitude and direction of the net force on the test charge, and what “causes” it?
- Now consider how all this looks in the reference frame of the test charge, where it’s at rest. In THIS frame, what is the magnetic force on the test charge $Q$? In this frame, it’s the negative charges in the wire that are moving to the left. Because they’re moving, the average distance between them is length-contracted. Meanwhile the positive charges are now at rest, so the average distance between them is now longer than $l$.
- What is the average distance ($l_+$) between the positive charge carriers in this frame? Both of these effects give the wire a non-zero charge density.
- Compute the charge density (charge per length) in this frame, with the correct overall sign.
- Use Gauss’s Law to compute the electrostatic force on the test charge.
- In THIS frame, what is the magnitude and direction of the force on the test charge, and what “causes” it?
- For normal currents, $\beta = v/c$ is about $10^{−13}$. (Drift velocities are small!) Given this, show that the forces you computed in parts 4 and 9 are the same size. Hint: expand in a Taylor series.
2. E&B transformations
\[\bar{E}_{x} = E_{x} \qquad \bar{E}_y = \gamma\left(E_y-vB_z\right) \qquad \bar{E}_z = \gamma\left(E_z+vB_y\right)\] \[\bar{B}_{x} = B_{x} \qquad \bar{B}_y = \gamma\left(B_y+\dfrac{v}{c^2}E_z\right) \qquad \bar{B}_z = \gamma\left(B_z-\dfrac{v}{c^2}E_y\right)\]- Use these equations to show that both $\mathbf{E}\cdot\mathbf{B}$ and $(E^2 − c^2 B^2)$ are Lorentz invariants.
- We found earlier that $\mathbf{E}$ and $\mathbf{B}$ are mutually perpendicular for traveling EM waves. Given that this is true in some frame, can there be any other reference frame in which you would find $\mathbf{E}$ and $\mathbf{B}$ not perpendicular for traveling EM waves?
- Suppose $E > cB$ in some frame. Show that there is no possible frame in which $E=0$.
- If $E = 0$ in some frame, do these relations mean that $E$ is always equal to 0 in every other inertial frame?
- If $B = 0$ (but $E$ is nonzero) in some frame, can you always (ever?) find another frame in which $E = 0$ (but $B$ is nonzero)?
3. Maxwell’s equations written compactly
We found that we could write the field tensor like this
\[F^{\mu\nu}=\left( \begin{array}{cccc} 0 & E_x/c & E_y/c & E_z/c\\ -E_x/c & 0 & B_z & -B_y\\ -E_y/c & -B_z & 0 & B_x\\ -E_z/c & B_y & -B_x & 0\\ \end{array} \right)\]and the dual tensor like this,
\[G^{\mu\nu}=\left( \begin{array}{cccc} 0 & B_x & B_y & B_z\\ -B_x & 0 & -E_z/c & E_y/c\\ -B_y & E_z/c & 0 & -E_x/c\\ -B_z & -E_y/c & E_x/c & 0\\ \end{array} \right)\]With the current density 4-vector written as this: $J^{\mu} = (c\rho,J_x,J_y,J_z)$, we claim that Maxwell’s equations in vaccuum are given thusly,
\[\dfrac{\partial F^{\mu\nu}}{\partial x^{\nu}} = \mu_0 J^{\mu}, \qquad \dfrac{\partial G^{\mu\nu}}{\partial x^{\nu}} = 0\]- Show by explicit calculation that you can recover all 4 Maxwell’s equations.
- What would have happened if $\dfrac{\partial G^{\mu\nu}}{\partial x^{\nu}} \neq 0$? Think about what happens physically?! It must be zero!