Announcements¶
- Homework 5 Working with Tensorflow. Due 12/4. This is the last homework assignment!
- Projects Rubric posted to D2L.
- Due finals week
- 8-10 minute video presentation + documented notebook on your analysis
- 3 In-class work periods for the project
Calendar¶
This week¶
- Thursday: Day 19 Perceptron model
Thanksgiving week¶
- Tuesday 11/24: Project work day 1
- Thursday 11/26: No class
Week after Thanksgiving¶
- Tuesday 12/1: Day 20 Neural Networks 1
- Thursday 12/3: Day 21 Neural Networks 2
Last week of classes¶
- Tuesday 12/8: Project work day 2
- Thursday 12/10: Project work day 3
Pre-Class¶
- What is the perceptron model doing?
- How do we take the mathematics and make it into code?
- How is this different from a neural network?
Perceptron (single layer neural network)¶
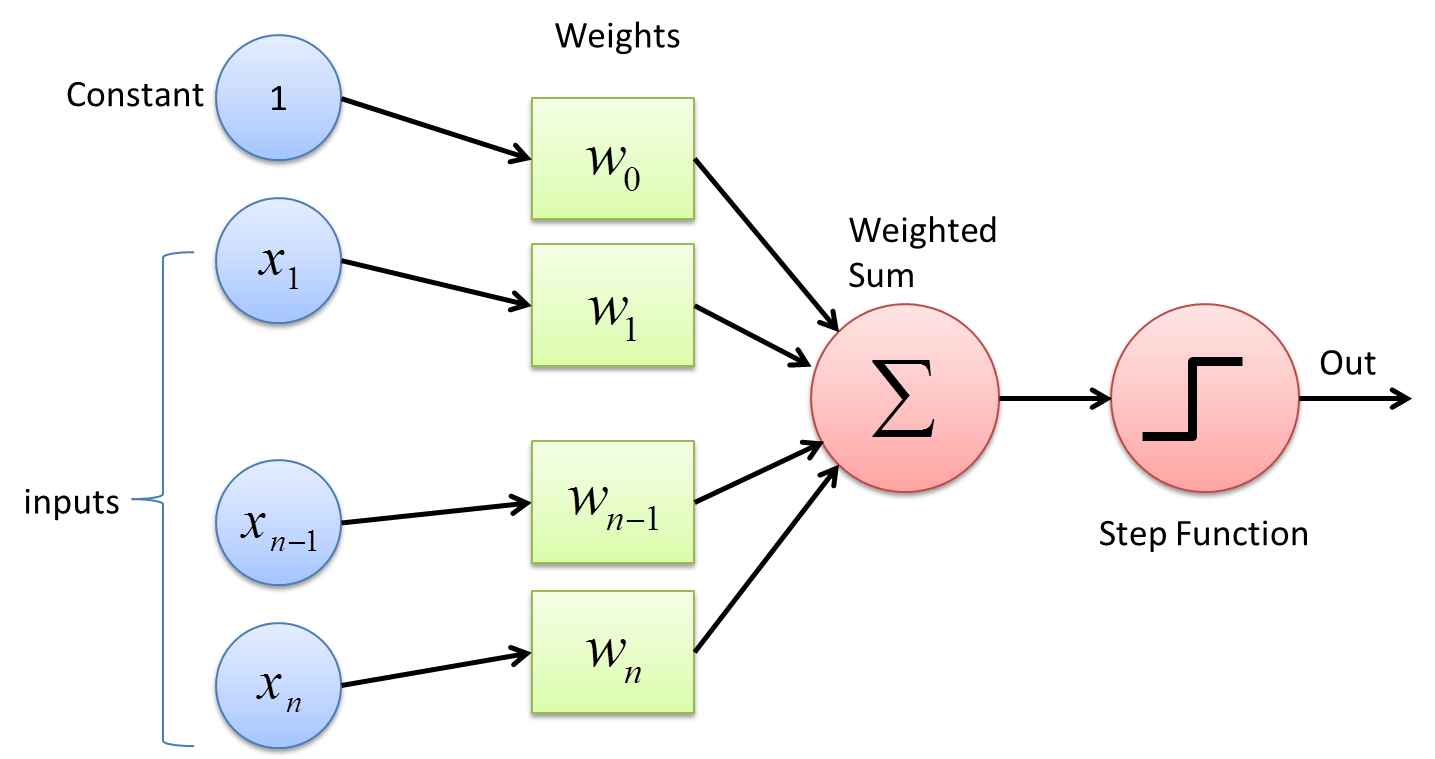
Neural Network ("multi layer perceptron")¶

How does a Perceptron model classify points?¶
2D example¶
- A perceptron model is trying to find a line to seperate the classes
- Each point in a 2D space has a location $(x_1, x_2)$; basically
feature_1andfeature_2 - A line in that space would have the normal form $A + Bx_1 + Cx_2 = 0$ or $x_2 = -\dfrac{B}{C}x_1 - \dfrac{A}{C}$
- Using an iterative approach, a Perceptron model tries to find $A$, $B$, and $C$.
One prediction predict()¶
The perceptron model iteratively determines $A$, $B$, and $C$ by looking at every point in the data it is trained on.
- Take the location of one data point plus a constant (the "bias"; e.g., 1) and take the dot product with an initial guess of the weights (e.g., $\vec{w} = (1,1,1)$). $$ result = \vec{x} \cdot \vec{w} = (x_1, x_2, 1) \cdot (1,1,1) = x_1 + x_2 + 1$$
- If $x_1 = 2$ and $x_2 = 3$, then the $result = (2+3+1) = 6$
Because this is greater than zero, we predict it to be in class 1
if result > 0:
predict class 1 and return 1;
else:
predict class 2 and return -1
For our example, we return 1!
But we know the class (because we are using supervised learning)!
Compare to actual class and update weights¶
- Originally we guessed the weights $\vec{w} = (1,1,1)$, we can use the misclassifications to update the weights.
Let's assume we were wrong, so the data is actually in class 2.
That update uses this equation:
$$ \vec{w}_{new} = \vec{w}_{old} + \eta*d*\vec{x}$$
where $\eta$ is the learning rate and $d$ = actual_class_value - predicted_class_value (as long as classes are 1 and -1)
Continuing example¶
We predicted class 1 (class_label=1), but the data is in class 2 (class_label=-1). So the update to the weights is:
where we choose $\eta$, let's take it to be 0.01. So the update is:
$$update = (-4,-6,-2)*0.01 = (-0.04, -0.06, -0.02)$$We add this to the guessed weights:
$$ \vec{w}_{new} = \vec{w}_{old} + update = (1,1,1) + (-0.04, -0.06, -0.02) = (0.96,0.94,0.98)$$What is we guess correctly?¶
In that case, the predicted and known classes are the same, so the update is:
$$update = \eta*d*\vec{x} = \eta*(-1 - (-1))*(2,3,1)$$$$update = \eta*(0)*(2,3,1) = (-4,-6,-2)*\eta = 0$$And there's no change to the weights because we did ok!
This means perceptrons don't find the "best line" just a line that separates the data.
So how do we fit the model? fit()¶
for the number of iterations we choose:
for the data we have:
predict the class
update the weights
